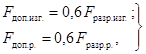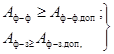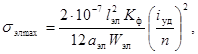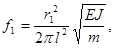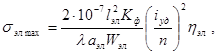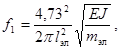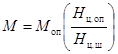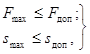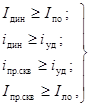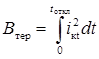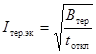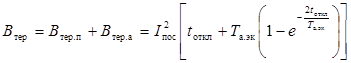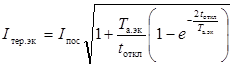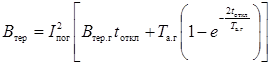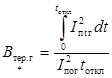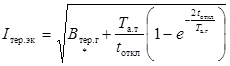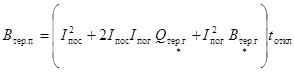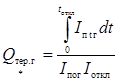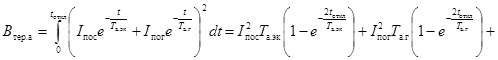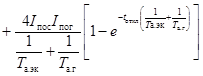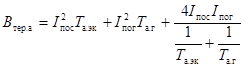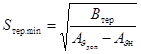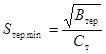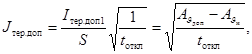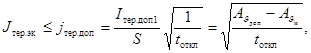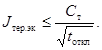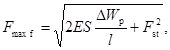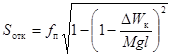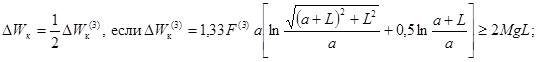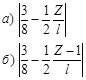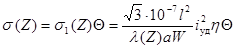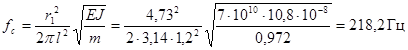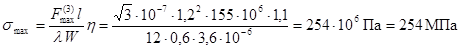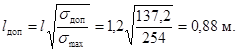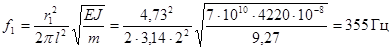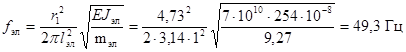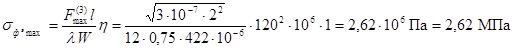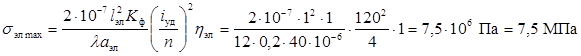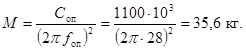ГОСТ 30323-95
ГОСТ Р 50254-92
МЕЖГОСУДАРСТВЕННЫЙ
СТАНДАРТ
КОРОТКИЕ ЗАМЫКАНИЯ
В ЭЛЕКТРОУСТАНОВКАХ
Методы расчета
электродинамического
и термического действия тока короткого замыкания
МЕЖГОСУДАРСТВЕННЫЙ
СОВЕТ
ПО СТАНДАРТИЗАЦИИ, МЕТРОЛОГИИ И СЕРТИФИКАЦИИ
Минск
ГОСТ 30323-95
ГОСТ Р 50254-92
МЕЖГОСУДАРСТВЕННЫЙ
СТАНДАРТ
КОРОТКИЕ ЗАМЫКАНИЯ В
ЭЛЕКТРОУСТАНОВКАХ
Методы расчета
электродинамического и термического действия
тока короткого замыкания
Short circuit in electrical installations.
Calculation methods of thermal and electrodynamic
effects of short circuit currents
Дата введения 1994-01-01
Настоящий стандарт распространяется на
трехфазные электроустановки промышленной частоты и определяет общую методику
расчета и проверки проводников и электрических аппаратов на электродинамическую
и термическую стойкость при коротких замыканиях.
Все пункты основного текста стандарта
являются обязательными, а приложения - рекомендуемыми.
1.1 Выбор расчетных условий КЗ
1.1.1 При проверке проводников и
электрических аппаратов электроустановок на электродинамическую и термическую
стойкость при КЗ предварительно должны быть выбраны расчетные условия КЗ, т.е.
расчетная схема электроустановки, расчетный вид КЗ в электроустановке, расчетная
точка КЗ, а также расчетная продолжительность КЗ в электроустановке (последнюю
используют при проверке на термическую стойкость проводников и на
невозгораемость кабелей).
1.1.2 Расчетная схема электроустановки
должна быть выбрана на основе анализа возможных электрических схем этой
электроустановки при продолжительных режимах ее работы. К последним следует
относить также ремонтные и послеаварийные режимы работы.
1.1.3 Расчетным видом КЗ следует
принимать:
- при проверке электрических аппаратов и
жестких проводников на электродинамическую стойкость - трехфазное КЗ;
- при проверке электрических аппаратов и
проводников на термическую стойкость - трех- или однофазное КЗ, а на
генераторном напряжении электростанций - трех- или двухфазное КЗ, в зависимости
от того, какое из них приводит к большему термическому воздействию;
- при проверке гибких проводников по
условию их допустимого сближения во время КЗ - трех- или двухфазное КЗ, в
зависимости от того, какое из них приводит к большему сближению проводников.
1.1.4 В качестве расчетной точки КЗ
следует принимать такую точку на расчетной схеме, при КЗ в которой проводник
или электрический аппарат подвергается наибольшему электродинамическому или
термическому воздействию.
Примечание. Исключения из этого требования
допустимы лишь при учете вероятностных характеристик КЗ и должны быть
обоснованы соответствующими ведомственными нормативно-техническими документами
(НТД).
1.1.5 Расчетную
продолжительность КЗ при проверке проводников и электрических аппаратов на
термическую стойкость следует определять путем сложения времени действия
основной релейной защиты, в зону которой входят проверяемые проводники и
электрические аппараты, и полного времени отключения соответствующего
выключателя, а при проверке кабелей на невозгораемость - путем сложения времени
действия резервной релейной защиты и полного времени отключения ближайшего к
месту КЗ выключателя.
При наличии устройств автоматического повторного
включения (АПВ) цепи следует учитывать суммарное термическое действие тока КЗ.
1.1.6 При расчетной продолжительности КЗ
до 1 с допустимо процесс нагрева проводников под действием тока КЗ считать
адиабатическим, а при расчетной продолжительности КЗ более 1 с и при
небыстродействующих АПВ следует учитывать теплоотдачу в окружающую среду.
2.1.1 Электродинамические силы
взаимодействия двух параллельных проводников конечного сечения (F)
в ньютонах следует определять
по формуле
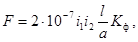 (1)
(1)
где 2×10-7
- постоянный параметр, Н/А2;
а - расстояние между осями проводников, м;
i1, i2 - мгновенные значения
тока проводников, А;
l -
длина проводников, м;
Кф -
коэффициент формы.
Для проводников прямоугольного сечения
коэффициент формы следует определять по кривым, приведенным на рисунке 1.
Диаграмма для определения
коэффициентов формы шин прямоугольного сечения
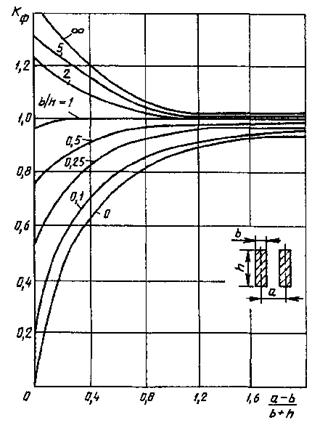
Рисунок 1
Для круглых проводников сплошного
сечения, проводников кольцевого сечения, а также проводников (шин) корытного
сечения с высотой сечения 0,1 м и более следует принять Кф
= 1,0.
2.1.2 Наибольшее значение
электродинамической силы имеет место при ударном токе КЗ.
2.1.3 Максимальную силу (F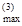 )
в ньютонах (эквивалентную равномерно распределенной по длине пролета
нагрузки), действующую в трехфазной системе проводников на расчетную фазу при
трехфазном КЗ, следует определять по формуле
)
в ньютонах (эквивалентную равномерно распределенной по длине пролета
нагрузки), действующую в трехфазной системе проводников на расчетную фазу при
трехфазном КЗ, следует определять по формуле
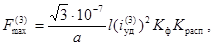 (2)
(2)
где ![]() - ударный ток трехфазного КЗ, А;
- ударный ток трехфазного КЗ, А;
![]() -
коэффициент, зависящий от взаимного расположения проводников;
-
коэффициент, зависящий от взаимного расположения проводников;
а - расстояние между осями проводников, м;
l - длина пролета, м.
Значения коэффициента 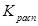 некоторых
типов шинных конструкций (рисунок 2) указаны в таблице 1.
некоторых
типов шинных конструкций (рисунок 2) указаны в таблице 1.
Схемы взаимного
расположения шин
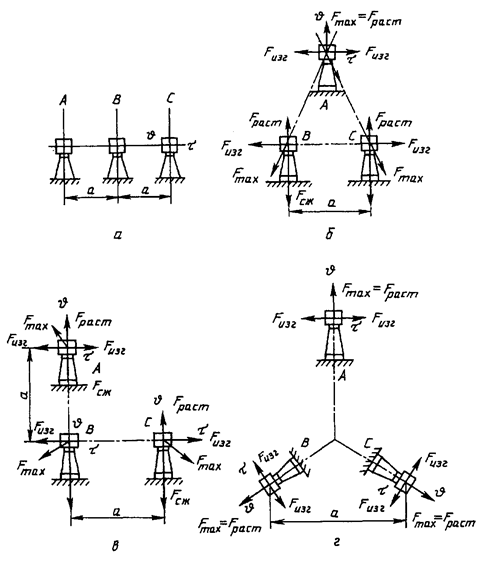
Рисунок 2
Таблица 1 - Значения коэффициента ![]()
|
Расположение шин
|
Расчетная
фаза
|
Значение
коэффициента ![]() для нагрузок для нагрузок
|
|
результирующей
|
изгибающей
|
растягивающей
|
сжимающей
|
|
1 В одной плоскости (рисунок 2а)
|
В
|
1,00
|
1,00
|
0
|
0
|
|
2 По вершинам равностороннего треугольника (рисунок 2б)
|
А
|
1,00
|
0,94
|
0,25
|
0,75
|
|
В
|
1,00
|
0,50
|
1,00
|
0
|
|
С
|
1,00
|
0,94
|
0,25
|
0,75
|
|
3 По вершинам прямоугольного равнобедренного треугольника (рисунок 2в)
|
А
|
0,87
|
0,87
|
0,29
|
0,87
|
|
В
|
0,95
|
0,43
|
0,83
|
0,07
|
|
С
|
0,95
|
0,93
|
0,14
|
0,43
|
|
4 По вершинам равностороннего треугольника (рисунок 2г)
|
А,
В, С
|
1,00
|
0,50
|
1,00
|
0
|
При двухфазном КЗ
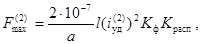 (3)
(3)
где 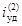 - ударный ток двухфазного КЗ, А.
- ударный ток двухфазного КЗ, А.
2.2.1 Методику расчета
электродинамической стойкости шинных конструкций и гибких токопроводов следует
выбирать на основе расчетной механической схемы, учитывающей их особенности.
2.2.2 Следует различать:
- статические системы, обладающие высокой
жесткостью, у которых шины и изоляторы при КЗ остаются неподвижными;
- динамические системы с жесткими
опорами, у которых изоляторы при КЗ могут считаться неподвижными, а шины
колеблются;
- динамические системы с упруго
податливыми опорами, в которых при КЗ колеблются шины и опоры;
- динамические системы с гибкими
проводами.
2.2.3 Расчетные механические схемы шинных
конструкций различных типов, обладающих высокой жесткостью, представлены в таблице
2.
Таблица 2
- Расчетная схема шинных конструкций
|
Номер схемы
|
Расчетная
схема
|
Тип
балки и опоры
|
Коэффициенты
|
|
l
|
b
|
r1
|
|
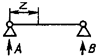
1
|
|
Однопролетная
А и B - изоляторы-опоры
|
8
|
1
|
3,14
|
|
2
|
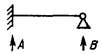
|
Однопролетная
А - защемление шины; В - изолятор-опора
|
8
|
1,25
|
3,93
|
|
3
|

|
А
и В - защемление шины на жестких опорах
|
12
|
1
|
4,73
|
|
4
|
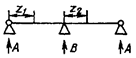
|
Балка
с двумя пролетами
|
8
|
1,25
|
3,93
|
|
5
|
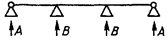
|
Балка
с тремя и более пролетами
|
10*
12**
|
1,13
1
|
4,73
|
|
* Для крайних пролетов,
** Для средних пролетов.
|
|
|
|
|
|
|
|
Расчетные схемы имеют вид
равнопролетной балки, лежащей или закрепленной на жестких опорах и
подвергающейся воздействию равномерно распределенной нагрузки.
Различают следующие типы шинных
конструкций и соответствующих расчетных механических схем:
- шинные конструкции с разрезными шинами,
длина которых равна длине одного пролета; расчетной схемой для них является
балка с шарнирным опиранием на обеих опорах пролета (таблица 2, схема 1);
- шинные конструкции с разрезными шинами,
длина которых равна длине двух пролетов, с жестким креплением на средней опоре;
расчетной схемой для них является балка с жестким опиранием (защемлением) на
одной и шарнирным на другой опоре пролета (таблица 2, схема 2);
- многопролетная шинная конструкция с
неразрезными шинами; расчетной схемой для средних пролетов является балка с
жестким опиранием (защемлением) на обеих опорах пролета (таблица 2, схема
3);
- шинные конструкции с разрезными шинами,
длина которых равна двум, трем и более пролетам, без жесткого крепления на
промежуточных опорах; расчетной схемой для них являются соответственно схемы 4
и 5 (таблица 2).
2.2.4 Расчетной схемой шинной конструкции
с упруго податливыми опорами следует считать схему, в которой масса шины
распределена по длине пролета, а опоры представлены телами с эквивалентной
массой М и пружинами с жесткостью Соп.
2.2.5 Для гибких токопроводов в качестве
расчетной схемы применяют схему с жестким стержнем, ось которого очерчена по
цепной линии. Гирлянды изоляторов вводят в механическую схему в виде жестких
стержней, шарнирно соединенных с проводами и опорами. Размеры стержней,
расчетной схемы определяют из статического расчета на действие сил тяжести.
2.3.1 Допустимое напряжение в материале
жестких шин (sдоп) в
паскалях следует принимать равным 70 % от временного сопротивления разрыву
материала шин sр
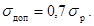 (4)
(4)
Допустимые напряжения в материале шин
следует принимать ниже пределов текучести этого материала.
Временные сопротивления разрыву и
допускаемые напряжения в материалах шин приведены в таблице 3.
В случае сварных шин их временное
сопротивление разрыву снижается. Значения временных сопротивлений разрыву в
области сварных соединений определяют экспериментально; при отсутствии
экспериментальных данных эти значения и значения допустимых напряжений следует
принимать, используя данные таблицы 3.
Таблица 3 - Основные
характеристики материалов шин
|
Материал шины
|
Марка
|
Временное
сопротивление разрыву, МПа
|
Допустимое
напряжение, МПа
|
Модуль
упругости, 1010 Па
|
|
материала
|
в
области сварного соединения
|
материала
|
в
области сварного соединения
|
|
1 Алюминий
|
А0,
А
АД0
|
118
59-69
|
118
59-69
|
82
41-48
|
82
41-48
|
7
7
|
|
2 Алюминиевый
сплав
|
АД31Т
|
127
|
120
|
89
|
84
|
7
|
|
АД31Т1
|
196
|
120
|
137
|
84
|
7
|
|
АВТ1
|
304
|
152
|
213
|
106
|
7
|
|
1915T
|
353
|
318
|
247
|
223
|
7
|
|
3 Медь
|
МГМ
|
245-255
|
-
|
171,5-178
|
-
|
10
|
|
МГТ
|
245-294
|
-
|
171,5-206
|
-
|
10
|
2.3.2
Допустимую нагрузку на изолятор (изоляционную опору) (Fдоп) следует принимать
равной 60 % от минимальной разрушающей нагрузки Fразр, приложенной
к вершине изолятора (опоры) при изгибе или разрыве
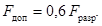 (5)
(5)
2.3.3 В зависимости от взаимного
расположения шин и изоляторов последние подвергаются воздействию
электродинамических сил, работая на изгиб или растяжение (сжатие) или
одновременно на изгиб и растяжение (сжатие). Допустимые нагрузки на изоляторы
при изгибе (Fдоп.изг.) и растяжении (Fдоп.р ) в ньютонах в этих случаях следует принимать соответственно
равными:
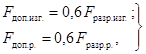 (6)
(6)
где Fразр.изг. и Fразр.р -
задаваемые предприятием-изготовителем минимальные разрушающие нагрузки
соответственно при изгибе и растяжении (сжатии) изолятора, Н.
2.3.4 Допустимую
нагрузку на спаренные изоляторы (опоры) следует принимать равной 50 % от
суммарного разрушающего усилия изоляторов (опор)
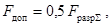 (7)
(7)
где Fразр å - суммарное разрушающее усилие спаренных изоляторов
(опор), Н.
2.3.5 Допустимую нагрузку при изгибе
опорного изолятора (Fдоп) в ньютонах следует определять в соответствии с
формулой
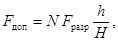 (8)
(8)
где N - коэффициент допустимой нагрузки, равный
0,6 или 0,5 (см. пп. 2.3.2-2.3.4);
h
и H - расстояния от опасного сечения изолятора
соответственно до его вершины и центра тяжести поперечного сечения шины (см.
рисунок 3),
м.
Опасное сечение опорно-стержневых
изоляторов с внутренним креплением арматуры (рисунок 3а) следует принимать у опорного
фланца, опорно-стрежневых изоляторов с внешним креплением арматуры (рисунки 3б, в) -
у кромки нижнего фланца, а опорно-штыревых изоляторов (рисунок 3г) - на
границе контакта штыря с фарфоровым телом изолятора.
Допустимую изгибающую нагрузку
многоярусных изоляционных опор (рисунки 3в, г) следует принимать равной
допустимой нагрузке наименее прочного яруса, определенной по формуле (8).
2.3.6 При расположении фаз по вершинам
треугольника (рисунки 2б, в, г) изоляторы одновременно испытывают как
растягивающие (сжимающие), так и изгибающие усилия. Допустимую изгибающую
нагрузку (Fдоп.изг) в
ньютонах следует определять по формуле (8), принимая Fразр равной разрушающей нагрузке при изгибе изолятора;
допустимую растягивающую нагрузку (Fдоп.р) следует определять по формуле (5),
принимая Fразр равной разрушающей нагрузке при растяжении.
2.3.7 Допустимое напряжение в материале
проводников (sдоп) в
мегапаскалях следует принимать равным
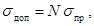
где sпр - предел прочности при растяжении, Н;
N - коэффициент допустимой нагрузки, равный 35-50 % от предела прочности.
К определению допустимых нагрузок на изоляторы и
шинные опоры
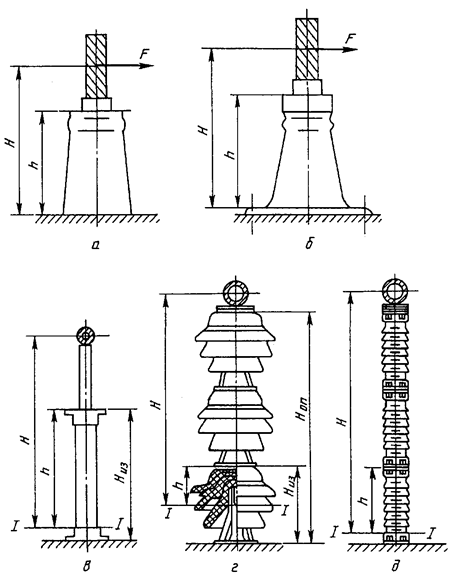
Рисунок 3
2.3.8 Допустимую нагрузку на подвесные
изоляторы следует принимать равной 30 % от разрушающей нагрузки, т.е.
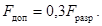 (9)
(9)
2.3.9 Расстояния между проводниками фаз (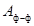 ) а также
между проводниками и заземленными частями (
) а также
между проводниками и заземленными частями (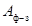 ) шинных конструкций
напряжением 35 кВ и выше и проводов ошиновки распределительных устройств,
воздушных линий и токопроводов к моменту отключения КЗ должны оставаться больше
допустимых изоляционных расстояний, определяемых при рабочих напряжениях
) шинных конструкций
напряжением 35 кВ и выше и проводов ошиновки распределительных устройств,
воздушных линий и токопроводов к моменту отключения КЗ должны оставаться больше
допустимых изоляционных расстояний, определяемых при рабочих напряжениях
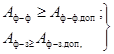 (10)
(10)
где 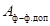 и
и 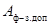 - минимально допустимые
расстояния по условиям пробоя соответственно между проводниками фаз и
проводниками и заземленными частями при рабочем напряжении.
- минимально допустимые
расстояния по условиям пробоя соответственно между проводниками фаз и
проводниками и заземленными частями при рабочем напряжении.
2.4.1 Расчет шинных конструкций, обладающих
высокой жесткостью
2.4.1.1 При расчете шинной конструкции,
обладающей высокой жесткостью, шину в любом пролете между изоляторами, кроме
крайних, следует рассматривать как стержень (балку с шарнирно опертыми концами,
таблица 2).
Наличие ответвлений допускается не учитывать.
2.4.1.2 Максимальное напряжение в
материале шины (smax) в паскалях и нагрузку на изолятор шинной конструкции
высокой жесткости при трехфазном КЗ (![]() ) в ньютонах следует определять
по формулам:
) в ньютонах следует определять
по формулам:
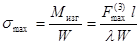 (11)
(11)
и
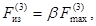 (12)
(12)
где ![]()
![]() - максимальная сила, возникающая
в многопролетной балке при трехфазном КЗ, Н, и определяемая по формуле (2);
- максимальная сила, возникающая
в многопролетной балке при трехфазном КЗ, Н, и определяемая по формуле (2);
l - длина пролета шин, м;
W- момент сопротивления поперечного сечения
шины, м3; формулы для его
расчета приведены в таблице 4;
l и b - коэффициенты, зависящие от
условия опирания (закрепления) шин, а также числа пролетов конструкции с
неразрезными шинами (таблица 2).
При двухфазном КЗ
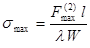 (13)
(13)
и
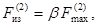 (14)
(14)
где ![]() - максимальная
сила, возникающая в многопролетной балке при двухфазном КЗ, Н, и определяемая
по формуле (3).
- максимальная
сила, возникающая в многопролетной балке при двухфазном КЗ, Н, и определяемая
по формуле (3).
Двухполосная шина
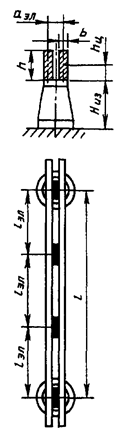
Рисунок 4
При расчете напряжений в области сварных соединений,
находящихся на расстоянии z
от опорного сечения, в формулы (11) и (13)
следует подставлять значения 1/l (z),
вычисленные в соответствии с таблицей
10.
2.4.1.3 Электродинамические нагрузки на
отдельные проводники составных шин (рисунок 4) обусловлены взаимодействием
проводников других фаз и отдельных элементов проводника одной фазы.
Максимальное напряжение в материале составных шин при КЗ допускается определять
по формуле
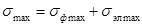 , (15)
, (15)
где 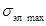 - максимальное напряжение в материале
шины, обусловленное взаимодействием проводников других фаз, Па, которое следует
определять в зависимости от вида КЗ по формуле (11) и (13);
- максимальное напряжение в материале
шины, обусловленное взаимодействием проводников других фаз, Па, которое следует
определять в зависимости от вида КЗ по формуле (11) и (13);
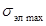 - максимальное напряжение в материале шины, обусловленное
взаимодействием отдельных элементов проводника одной фазы, Па, которое следует
определять по формуле
- максимальное напряжение в материале шины, обусловленное
взаимодействием отдельных элементов проводника одной фазы, Па, которое следует
определять по формуле
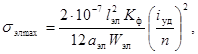 (16)
(16)
где 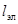 - длина пролета элемента шины между
прокладками, м;
- длина пролета элемента шины между
прокладками, м;
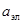 - расстояние между осями
поперечных сечений элементов составных шин (рисунок 4), м;
- расстояние между осями
поперечных сечений элементов составных шин (рисунок 4), м;
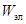 - момент сопротивления
поперечного сечения элемента шины, м3;
- момент сопротивления
поперечного сечения элемента шины, м3;
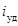 -
ударный ток трехфазного или двухфазного КЗ, А;
-
ударный ток трехфазного или двухфазного КЗ, А;
п - число составных проводников фазы.
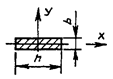
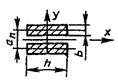
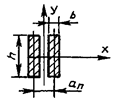
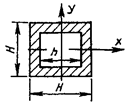
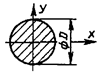
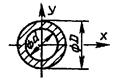
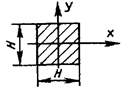
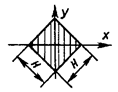
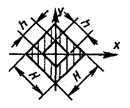
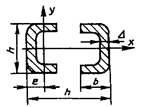
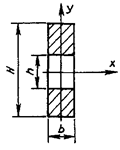
Таблица 4
- Формулы для определения момента инерции J и
момента сопротивления W поперечных сечений шин
|
Сечения шин
|
Расчетные
формулы
|
|
J, м4
|
W, м3
|
|
|
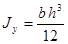
|
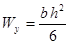
|
|
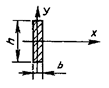
|
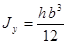
|
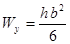
|
|
|
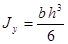
|
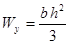
|
|
|
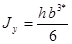
|
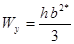
|
|
|
![]()
|
![]()
|
|
|
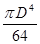
|
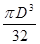
|
|
|
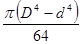
|
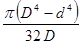
|
|
|
![]()
|
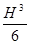
|
|
|
![]()
|
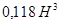
|
|
-
|
![]()
|
![]()
|
|
|
Для одного элемента
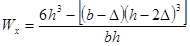
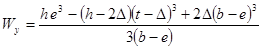
|
|
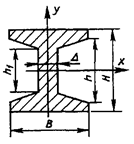
|
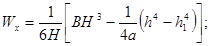
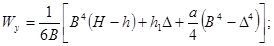
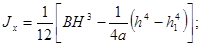
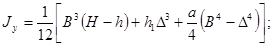
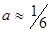 для
стандартных двутавровых профилей для
стандартных двутавровых профилей
|
|
|
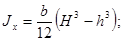
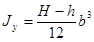
|
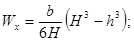
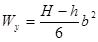
|
|
Сечение
прокатных профилей стандартных размеров
|
Приближенные
формулы:
двутавровый
профиль на «ребро»
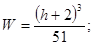
швеллерообразный
(корытный) профиль на «ребро»
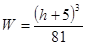
|
|
Сечение
любой формы
|
Ориентировочная
оценка момента сопротивления относительно центральной оси:
для сплошного
симметричного сечения
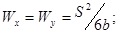 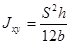
для полого
симметричного сечения
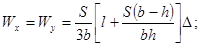
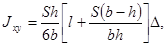
где S - площадь сечения; h, b - высота и ширина сечения соответственно; l - периметр; D - толщина стенки (для полого сечения)
|
|
* Если прокладки приварены к обеим полосам пакета,
момент инерции и момент сопротивления принимают равными:
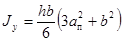 и и
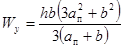
|
|
|
|
|
2.4.2 Расчет шинных конструкций с жесткими опорами
2.4.2.1 Шинную конструкцию, изоляторы
которой обладают высокой жесткостью, в расчетах на динамическую стойкость при
КЗ следует представлять как стержень с защемленными концами, имеющий лишь
основную частоту собственных колебаний.
2.4.2.2 Максимальное напряжение в материале
шин (smax) в паскалях и нагрузку на изоляторы (Fиз) в ньютонах при расположении шин в одной плоскости и
высокой жесткости изоляторов шинной конструкции следует определять по формулам
при трехфазном КЗ
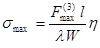 (17)
(17)
и
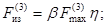 (18)
(18)
при двухфазном КЗ
![]()
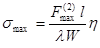 (19)
(19)
и
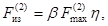 (20)
(20)
где h - коэффициент
динамической нагрузки, зависящий от расчетной основной частоты собственных
колебаний шины f1.
Значения коэффициента в зависимости от отклонения f1/fc
(fc = 50 Гц) следует определять
по графикам, приведенным на рисунке 5.
Значения расчетной частоты собственных
колебаний (fc)
в герцах следует определять в соответствии с 2.4.2.4.
Зависимость динамического
коэффициента для изоляторов и шин от частоты собственных колебаний шины
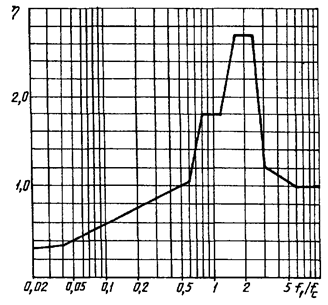
Рисунок 5
2.4.2.3 Максимальную нагрузку на
проходные изоляторы (Fиз) в
ньютонах следует определять по формуле
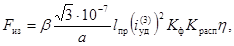 (21)
(21)
где lпр -
расстояние от торца проходного изолятора до ближайшего опорного изолятора фазы,
м.
2.4.2.4 Расчетную
частоту собственных колебаний шины (f1) в герцах следует определять по формуле
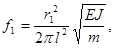 (22)
(22)
где Е - модуль упругости материала шины, Па;
J - момент инерции поперечного сечения шины, м4;
m - масса шины на единицу длины, кг/м;
r1 - параметр
основной частоты собственных колебаний шины. Значения этого параметра зависят
от типа шинной конструкции и представлены в таблице 2.
2.4.2.5 Максимальное напряжение в
материале составных шин (smax) в паскалях шинной конструкции с жесткими опорами
допустимо определять по формуле (15). При этом максимальное напряжение в материале
шин, обусловленное взаимодействием проводников других фаз (sф max) в паскалях, следует
определять в зависимости от вида КЗ по формуле (17) или (19), а
максимальное напряжение в материале шины, обусловленное взаимодействием
отдельных элементов проводника одной фазы (sэл max) в паскалях, - по формуле
![]()
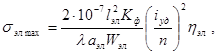 (23)
(23)
где hэл - коэффициент динамической нагрузки, зависящий от
расчетной основной частоты собственных колебаний элементов составной шины (f1 эл)который
следует определять по расчетным графикам, приведенным на рисунке 5.
Расчетную основную частоту собственных
колебаний элементов составной шины (f1эл) в герцах
следует определять по формуле
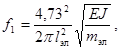 (24)
(24)
где lэл - длина
пролета элемента шины между прокладками, м;
J - момент инерции поперечного сечения элемента шин, м3;
mэл - масса элемента на единицу длины, кг/м;
аэл - расстояние между осями поперечных сечений элементов
составных шин (рисунок 4), м.
2.4.2.6 Максимальное напряжение в
материале шин (smax) в паскалях и максимальную нагрузку на опорные и проходные изоляторы (Fиз) в ньютонах, при
расположении шин по вершинам треугольника (рисунки 26, в, г), следует определять с
учетом их пространственных колебаний, используя формулы:
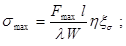 (24)
(24)
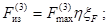 (25)
(25)
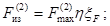 (26)
(26)
где W - меньший из двух моментов сопротивления поперечного
сечения шины (момента сопротивления wu при изгибе в плоскости u и момента
сопротивления Wt при изгибе шины в плоскости t (рисунок 2), м3;
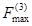 ,
,![]() - электродинамические силы,
определяемые соответственно по формулам (2) и (3);
- электродинамические силы,
определяемые соответственно по формулам (2) и (3);
xs , xF - коэффициенты,
значения которых для наиболее распространенных типов шинных конструкций
(рисунки 2б,
в, г) приведены в таблице 5.
Таблица 5 - Значения
коэффициентов xs и xF шинных конструкций
|
Расположение шин
|
Эскиз
конструкции на рисунке 2
|
Значение
коэффициента
xF
|
Значение
коэффициента xs
|
|
для
шин круглого и кольцевого сечений
|
для
шин квадратного сечения
|
|
1 По вершинам прямоугольного равнобедренного треугольника
|
в
|
0,95
|
0,95
|
1,16
|
|
2 По вершинам равностороннего треугольника
|
б
|
1,0
|
1,0
|
1,39
|
|
г
|
1,0
|
1,0
|
1,21
|
2.4.3 Расчет подвесного самонесущего токопровода
2.4.3.1 Расчетное максимальное напряжение
в материале шин подвесного самонесущего токопровода (sрасч max) в
паскалях следует определять с учетом собственной массы, массы изоляционных
распорок и льда, а также действия напора ветра, т.е.
sрасч max=smax + sВ ,
где smax -
максимальное напряжение в материале шин вследствие электродинамического
действия тока КЗ;
sВ -
напряжение в материале шин от собственной массы, массы изоляционных распорок и
льда, а также действия напора ветра.
Нагрузку на изолятор подвесного
самонесущего токопровода следует определять по формуле (12).
2.4.4 Расчет
шинных конструкций с упругоподатливыми опорами
2.4.4.1 Максимальное напряжение в
материале шин и максимальную нагрузку на изоляторы шинных конструкций с
упругоподатливыми опорами следует определять соответственно по формулам (17) и (18), а
частоту собственных колебаний - по формуле (22), учитывая при этом, что
параметр основной частоты r1 является функцией безразмерных величин Cопl3/EJ и
M/ml
где Соп - жесткость
опор, а М - приведенная масса. Значения жесткости опор определяют по
экспериментальным данным, а приведенной массы - согласно 2.4.4.2.
Кривые для определения r1 шин с
жестким закреплением на опорах приведены на рисунке 6, а для шин с шарнирным
закреплением - на рисунке 7. Для шин с чередующимися жесткими и шарнирными
закреплениями на опорах значение параметра r1 допустимо приблизительно оценивать как среднее между
его значениями, найденными по кривым рисунков 6 и 7.
Кривые для определения
параметра основной частоты собственных колебаний шины при ее жестком
закреплении на упругоподатливых опорах
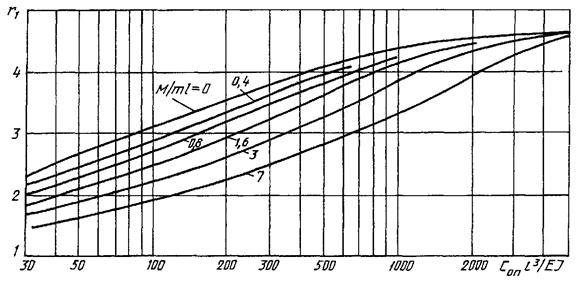
Рисунок 6
Кривые для определения
параметра основной частоты собственных колебаний шины при шарнирном закреплении
ее на упругоподатливых опорах
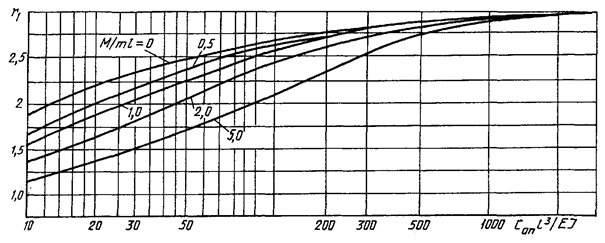
Рисунок 7
Значения r1 для шин с жестким закреплением на опорах при 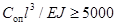 и для шин с
шарнирным закреплением на опорах при
и для шин с
шарнирным закреплением на опорах при 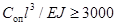 приведены в таблице 2.
приведены в таблице 2.
2.4.4.2 Приведенную
массу опоры (M) в
килограммах определяют по приближенной формуле
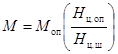 , (28)
, (28)
где Моп - масса опоры, кг;
Hц.оп и Hц.ш - расстояния от
основания опоры соответственно до центра массы опоры (изолятора) и центра массы
поперечного сечения шины (рисунок 8), м. Если частота собственных колебаний опоры,
закрепленной на упругом основании известна, то приведенную массу (М) в
килограммах следует определять по формуле
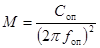 , (29)
, (29)
где Соп - жесткость опоры,
практически равная жесткости изолятора Сиз, Н/м;
fоп - частота собственных колебаний опоры, Гц, равная
частоте колебаний изолятора, Гц.
2.4.5 Проверка
токопроводов на электродинамическую стойкость при наличии устройств
автоматического повторного включения
2.4.5.1 При наличии быстродействующих АПВ
токопроводы электроустановок напряжением 35 кВ и выше следует проверять на
электродинамическую стойкость при повторном включении на КЗ.
Методика проверки приведена в приложении 4.
Такой проверки не требуется, если продолжительность бестоковой паузы, (tб.п) в секундах, составляет
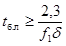 ,
,
где f1 - первая
(основная) частота собственных колебаний ошиновки, Гц;
d - декремент затухания токопровода при горизонтальных
колебаниях шин.
К расчету приведенной массы опоры
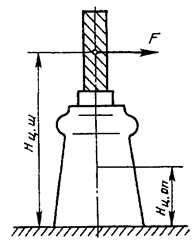
Рисунок 8
2.4.6 Расчет
гибких проводников
2.4.6.1 При расчете гибких проводников
следует определять максимальные тяжение в проводниках и отклонение проводников
при и после КЗ.
Расчет гибких проводников следует вести,
исходя из закона сохранения энергии. Предварительные оценки тяжений в
проводниках и смещений проводников допускается делать без учета влияния гирлянд
изоляторов.
Расчет гибких проводников следует вести с
помощью алгоритмов и программ на ЭВМ. Предварительные оценки тяжений в
проводниках и смещений проводников допускается делать на основе закона
сохранения энергии без учета расщепления проводников по методикам,
представленным в приложении 1.
2.5.1 При проверке шинных конструкций на
электродинамическую стойкость расчетными величинами являются максимальное
напряжение в материале шин (smax) в паскалях и максимальная нагрузка на изоляторы (Fmax) в ньютонах.
Для проверки электродинамической
стойкости шинных конструкций следует использовать следующие неравенства:
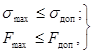 (30)
(30)
где sдоп - допустимое механическое напряжение в материале шин,
Па, которое следует определять в соответствии с п. 2.3;
Fдоп - допустимая механическая нагрузка на изоляторы, которую
следует определять в соответствии с указаниями п. 2.3.
2.5.2 При проверке гибких проводников на
электродинамическую стойкость расчетными величинами являются максимальное
тяжение Fmaxf отклонение
проводов при КЗ sотк.
Для проверки электродинамической
стойкости гибких проводников следует использовать следующие неравенства:
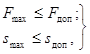 (31)
(31)
где Fдоп - допустимое тяжение проводов, которое следует
определять в соответствии с указаниями п. 2.3;
sдоп -
допустимое отклонение проводов, которое следует определять в соответствии с
указаниями п. 2.3.
2.5.3 Электродинамическая стойкость
электрических аппаратов в зависимости от типа и конструкции характеризуется их
предельными сквозными токами iпр.скв и Iпр.скв и номинальными
токами электродинамической стойкости iдин и Iдин или кратностью тока
электродинамической стойкости 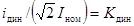 .
.
Электродинамическая стойкость
электрического аппарата обеспечена, если выполняются условия:
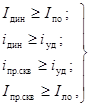 (32)
(32)
где Iпо -
начальное значение периодической составляющей тока КЗ в электрическом аппарате;
iуд -
ударный ток КЗ.
3.1.1 Степень термического воздействия
тока КЗ на проводники и электрические аппараты определяется значением интеграла
Джоуля (Втер) в амперах в квадрате на секунду
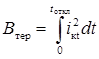 , (33)
, (33)
где iкt - ток КЗ в произвольный момент времени t,
А;
tоткл -
расчетная продолжительность КЗ в электроустановке (см. п. 1.1.5),
с.
Допустимо степень термического
воздействия тока КЗ определять также термически эквивалентным током КЗ
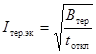 (34)
(34)
и расчетной продолжительностью КЗ.
3.1.2 Необходимый для проверки
проводников и электрических аппаратов на термическую стойкость при КЗ интеграл
Джоуля Bтер
допускается определять приближенно как сумму интегралов от периодической и
апериодической составляющих тока КЗ, т.е.
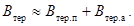 (35)
(35)
3.1.3 Методика аналитических расчетов
интеграла Джоуля и термически эквивалентного тока КЗ зависит от расчетной схемы
электроустановки, положения расчетной точки КЗ и ее удаленности от генераторов,
синхронных компенсаторов и электродвигателей. При этом возможны следующие
случаи:
а) исходная расчетная схема
электроустановки имеет произвольный вид, но для всех генераторов и синхронных
компенсаторов КЗ является удаленным, т.е. отношение действующего значения
периодической составляющей тока любого генератора или синхронного компенсатора
в начальный момент КЗ к его номинальному току менее двух. В этом случае все
источники электрической энергии путем преобразования схемы замещения должны
быть заменены одним эквивалентным источником, ЭДС которого принимают неизменной
по амплитуде, а индуктивное сопротивление равным результирующему эквивалентному
сопротивлению элементов расчетной схемы;
б) исходная расчетная схема содержит один
или несколько однотипных и одинаково удаленных от расчетной точки КЗ
генераторов (синхронных компенсаторов), причем расчетное КЗ является близким:
действующее значение периодической составляющей тока генератора (синхронного компенсатора)
превышает его номинальный ток в 2 и более раза;
в) исходная расчетная схема содержит
произвольное число источников энергии, для которых расчетное КЗ является
удаленным, а также генератор (синхронный компенсатор), который связан с точкой
КЗ по радиальной схеме и это КЗ для него является близким. При этом все
удаленные источники энергии и связывающие их с точкой КЗ элементы расчетной
схемы следует объединить в отдельную ветвь и эквивалентную ЭДС в этой ветви
считать неизменной по амплитуде;
г) исходная расчетная схема содержит
различные источники энергии, для которых расчетное КЗ является удаленным, и
группу электродвигателей, причем расчетная точка КЗ находится на шинах, к
которым подключены электродвигатели. При этом на схеме замещения все удаленные
источники энергии и связывающие их с точкой КЗ элементы расчетной схемы следует
объединить в отдельную ветвь и эквивалентную ЭДС в этой ветви считать
неизменной по амплитуде.
3.1.4 При определении интеграла Джоуля и
термической эквивалентного тока КЗ допускается принимать, что апериодическая
составляющая тока КЗ от той части расчетной схемы, которая содержит удаленные
от места КЗ источники энергии, независимо от ее конфигурации изменяется по
экспоненциальному закону с эквивалентной постоянной времени
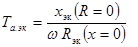 (36)
(36)
где хэк(R
= 0) и Rзк(х = 0) -
результирующие эквивалентные индуктивное и активное сопротивления
рассматриваемой части расчетной схемы, определяемые из схем замещения, в
которых все элементы расчетной схемы учтены соответственно только индуктивными
и только активными сопротивлениями.
3.1.5 Если исходная
расчетная схема содержит один или несколько источников энергии, для каждого из
которых расчетное КЗ является удаленным, то интеграл Джоуля (Втер)
в амперах в квадрате на секунду, следует определять по формуле
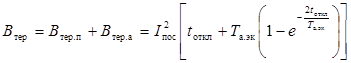 , (37)
, (37)
где Iпос -
начальное значение периодической составляющей тока КЗ от удаленного источника
(источников), А.
В этом случае термически эквивалентный
ток КЗ (Iтер.эк) в
амперах равен
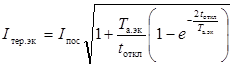 , (38)
, (38)
В случаях, когда 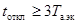 , интеграл Джоуля Bтер допустимо определять по
формуле
, интеграл Джоуля Bтер допустимо определять по
формуле
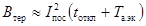 , (39)
, (39)
а термически эквивалентный ток КЗ (Iтер.эк) в амперах - по
формуле
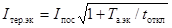 . (40)
. (40)
3.1.6 Если исходная расчетная схема
содержит один или несколько однотипных и одинаково удаленных от расчетной точки
КЗ генераторов (синхронных компенсаторов), причем расчетное КЗ является
близким, то интеграл Джоуля Bтер
следует определять по формуле
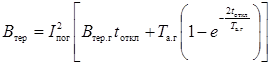 , (41)
, (41)
где Iпог -
начальное действующее значение периодической составляющей тока КЗ от генератора
(генераторов, синхронных компенсаторов), А;
Та.г - постоянная времени затухания апериодической
составляющей тока от генератора (генераторов, синхронных компенсаторов), с;
![]() -
относительный интеграл Джоуля:
-
относительный интеграл Джоуля:
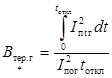 , (42)
, (42)
где tпtг - действующее значение периодической составляющей тока
КЗ от генератора (генераторов, синхронных компенсаторов) в произвольный момент
времени, А.
Значения относительного интеграла Джоуля ![]() ,
учитывающего влияние изменения во времени амплитуды периодической составляющей
тока КЗ, при разных системах возбуждения генераторов и разных удаленностях
расчетной точки КЗ от генераторов, т.е. разных отношениях действующего значения
периодической составляющей тока генератора в начальный момент КЗ к номинальному
току машины могут быть определены по кривым на рисунках 9-12.
,
учитывающего влияние изменения во времени амплитуды периодической составляющей
тока КЗ, при разных системах возбуждения генераторов и разных удаленностях
расчетной точки КЗ от генераторов, т.е. разных отношениях действующего значения
периодической составляющей тока генератора в начальный момент КЗ к номинальному
току машины могут быть определены по кривым на рисунках 9-12.
При рассматриваемой исходной расчетной
схеме термически эквивалентный ток КЗ (Iтер.эк) амперах следует определять по формуле
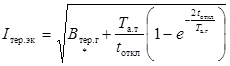 , (4)
, (4)
Кривые для определения ![]() от синхронных генераторов с
тиристорной или высокочастотной системой возбуждения
от синхронных генераторов с
тиристорной или высокочастотной системой возбуждения
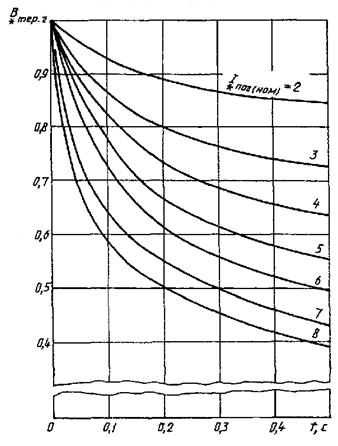
Рисунок 9
Кривые для определения ![]() от
синхронных генераторов с
тиристорной системой самовозбуждения и с последовательными трансформаторами
от
синхронных генераторов с
тиристорной системой самовозбуждения и с последовательными трансформаторами
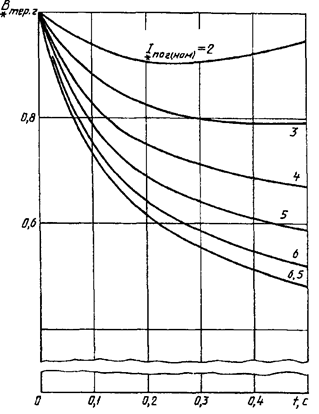
![]()
Рисунок 10
Кривые для определения ![]() от синхронных генераторов с
тиристорной системой самовозбуждения без последовательных трансформаторов
от синхронных генераторов с
тиристорной системой самовозбуждения без последовательных трансформаторов
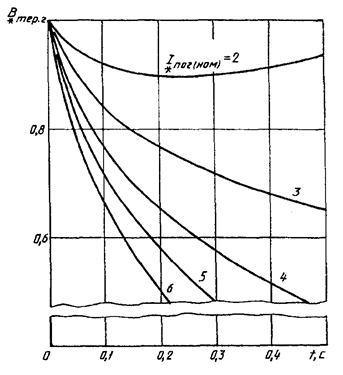
Рисунок 11
Кривые для определения ![]() от
синхронных генераторов с диодной бесщеточной системой возбуждения
от
синхронных генераторов с диодной бесщеточной системой возбуждения
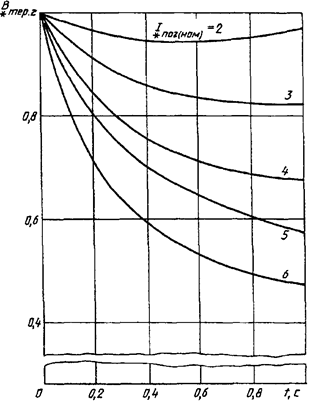
Рисунок 12
В случаях, когда 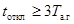 , интеграл
Джоуля Bтер
допустимо определять по формуле
, интеграл
Джоуля Bтер
допустимо определять по формуле
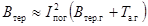 , (44)
, (44)
а термически эквивалентный ток КЗ (Iтер.эк) в амперах - по
формуле
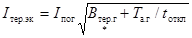 . (45)
. (45)
3.1.7 Если исходная
расчетная схема содержит произвольное число источников энергии, для которых
расчетное КЗ является удаленным, а также генератор (синхронный компенсатор),
который при КЗ оказывается связанным с точкой КЗ по радиальной схеме и это КЗ
для него является близким, то интеграл Джоуля от периодической составляющей
тока КЗ (Bтер.п) в
амперах в квадрате на секунду следует определять по формуле
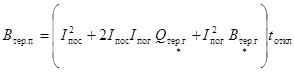 , (46)
, (46)
где Iпос -
начальное значение периодической составляющей тока КЗ от удаленных источников
энергии, А;
![]() -
относительный интеграл от периодической составляющей тока КЗ:
-
относительный интеграл от периодической составляющей тока КЗ:
![]()
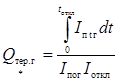 . (47)
. (47)
Значения относительного интеграла ![]() при разных
системах возбуждения генераторов и разных
удаленностях расчетной точки КЗ от генераторов могут быть определены по кривым
на рисунках 13-16.
при разных
системах возбуждения генераторов и разных
удаленностях расчетной точки КЗ от генераторов могут быть определены по кривым
на рисунках 13-16.
Кривые для определения ![]() от синхронных
генераторов с тиристорной или высокочастотной системой возбуждения
от синхронных
генераторов с тиристорной или высокочастотной системой возбуждения
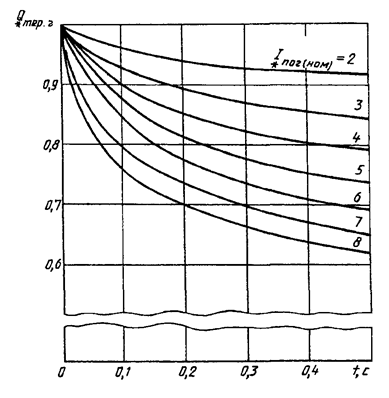
Рисунок 13
Кривые для определения ![]() от синхронных генераторов
с тиристорной системой самовозбуждения и с последовательными трансформаторами
от синхронных генераторов
с тиристорной системой самовозбуждения и с последовательными трансформаторами
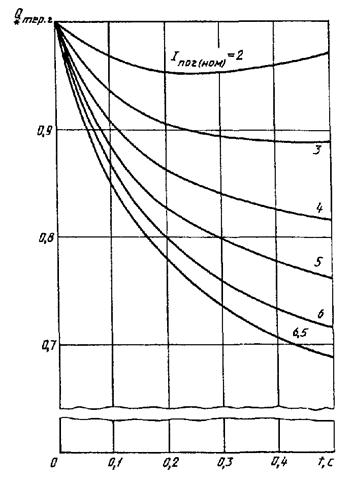
Рисунок 14
Кривые для определения ![]() от синхронных генераторов
с тиристорной системой самовозбуждения без последовательных трансформаторов
от синхронных генераторов
с тиристорной системой самовозбуждения без последовательных трансформаторов
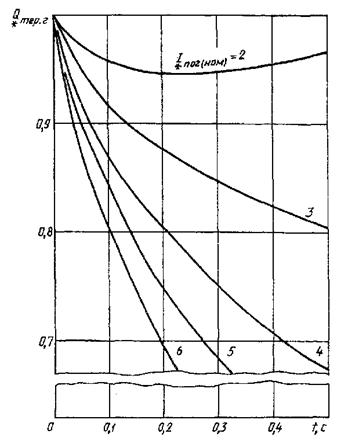
Рисунок 15
Кривые для определения ![]() от синхронных генераторов
с диодной бесщеточной системой возбуждения
от синхронных генераторов
с диодной бесщеточной системой возбуждения
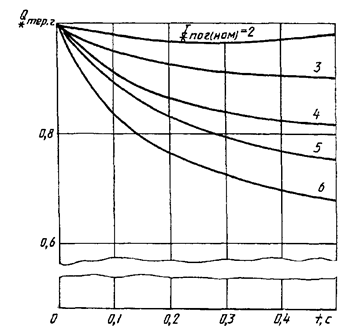
Рисунок 16
При определении интеграла Джоуля от
апериодической составляющей тока КЗ необходимо учитывать, что численные
значения постоянных времени затухания апериодических составляющих токов от
генератора или синхронного компенсатора (Та.г) в секундах
и от удаленных источников энергии (Та.эк) в секундах обычно
значительно отличаются друг от друга. Поэтому интеграл Джоуля следует
определять по выражению
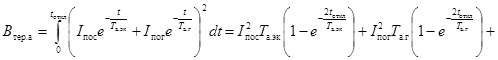
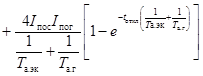 . (48)
. (48)
В случаях, когда tоткл 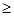 3Tа.г,допустимо использовать выражение
3Tа.г,допустимо использовать выражение
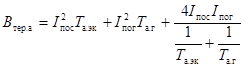 (49)
(49)
При рассматриваемой расчетной схеме
термически эквивалентный ток КЗ определяют по формуле (34), учитывая при этом (35). Значение Втер.п находят с
помощью формулы (46), а Bтер.а - с помощью формулы (48) или (49).
3.1.8 Если исходная
расчетная схема содержит удаленные от точки КЗ источники энергии и группу
электродвигателей, причем расчетная точка КЗ находится на шинах, к которым
подключены электродвигатели, то для упрощения расчета интеграла Джоуля группу
электродвигателей допустимо заменить одним эквивалентным электродвигателем,
мощность которого равна сумме номинальных мощностей отдельных электродвигателей.
При этом интеграл Джоуля следует определять по методике, изложенной в п.3.1.7, т.е. с использованием формул (46), (48), (49), в которые вместо Iпог, Tа.г, ![]() и
и ![]() следует
подставлять соответственно начальное значение периодической оставляющей тока КЗ
от эквивалентного двигателя Iпод,
постоянную времени затухания апериодической составляющей его тока Та.д
и функции
следует
подставлять соответственно начальное значение периодической оставляющей тока КЗ
от эквивалентного двигателя Iпод,
постоянную времени затухания апериодической составляющей его тока Та.д
и функции ![]() и
и
![]() для
этого электродвигателя. Значения этих функций для синхронных электродвигателей
могут быть определены по кривым на рисунках 17 и 18, а для
асинхронных электродвигателей - по кривым на рисунках 19 и 20.
для
этого электродвигателя. Значения этих функций для синхронных электродвигателей
могут быть определены по кривым на рисунках 17 и 18, а для
асинхронных электродвигателей - по кривым на рисунках 19 и 20.
Термически эквивалентный ток КЗ
определяют по формуле (34).
3.2.1 Термическая стойкость электрических
аппаратов при КЗ характеризуется их нормированным током термической стойкости (Iтер.норм) в амперах и
допустимым временем воздействия этого тока (tтер.норм) в секундах.
3.2.2 Расчетное выражение, которое
следует использовать при проверке коммутационных аппаратов на термическую
стойкость, зависит от расчетной продолжительности КЗ.
Если расчетная продолжительность КЗ (tоткл) в секундах равна или
больше допустимого времени воздействия нормированного тока термической
стойкости (tтер.норм)
в секундах, то для проверки коммутационных аппаратов следует использовать
выражение
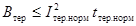 . (50)
. (50)
Если же tоткл<tтер.норм,
то условием термической стойкости является
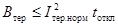 . (51)
. (51)
Кривые для определения ![]() от синхронного
электродвигателя
от синхронного
электродвигателя
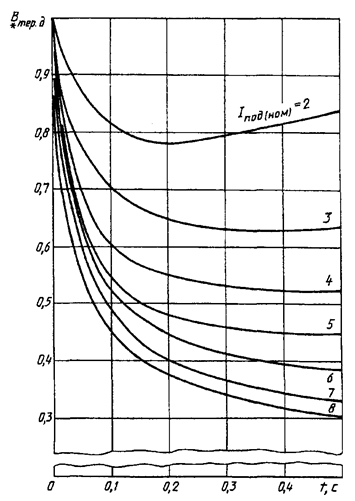
Рисунок 17
Кривые для определения ![]() от синхронного
электродвигателя
от синхронного
электродвигателя
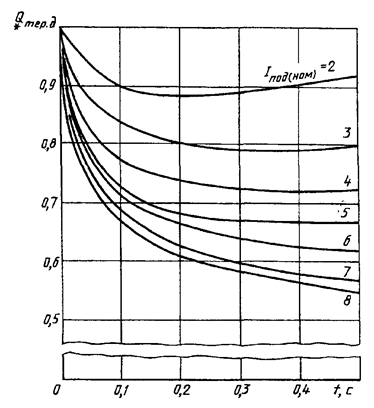
Рисунок 18
Кривые для определения ![]() от асинхронного
электродвигателя
от асинхронного
электродвигателя
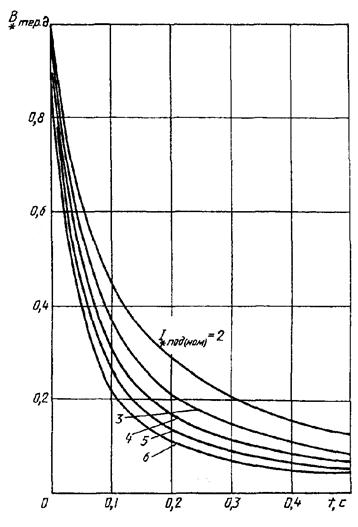
Рисунок 19
Кривые для определения ![]() от асинхронного
электродвигателя
от асинхронного
электродвигателя
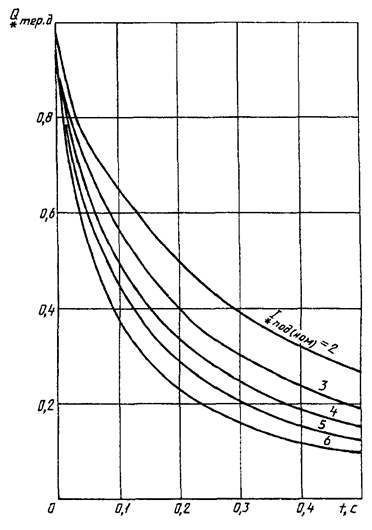
Рисунок 20
3.2.3 Допускается проверку коммутационных
электрических аппаратов на термическую стойкость при КЗ производить путем
сравнения термически эквивалентного тока КЗ с допустимым током термической
стойкости, учитывая при этом соотношение между допустимым временем воздействия
нормированного тока термической стойкости и расчетной продолжительностью КЗ.
Если tоткл>tтер.норм, то проверку коммутационных аппаратов на термическую
стойкость при КЗ следует производить, используя соотношение
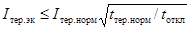 . (52)
. (52)
Если же tоткл<tр.норм, то
условием термической стойкости коммутационного аппарата является соотношение
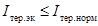 . (53)
. (53)
3.3.1 Проверка проводников на термическую
стойкость при КЗ заключается или в определении их температуры нагрева к моменту
отключения КЗ и сравнении этой температуры с предельно допустимой температурой
нагрева соответствующих проводников при КЗ, или в определении термически
эквивалентной плотности тока КЗ и сравнении этой плотности с допустимой
плотностью тока КЗ.
3.3.2 Расчет
температуры нагрева проводников к моменту отключения КЗ следует вести с
использованием кривых, приведенных на рисунке 21 - для жестких шин, кабелей и некоторых проводов, и
рисунке 22 - для проводов других
марок.
Кривые для определения температуры нагрева шин,
проводов и кабелей из различных материалов при КЗ
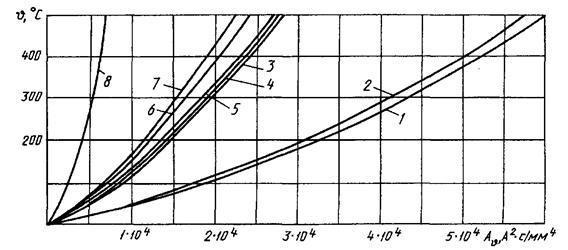
Материалы проводников: 1 - ММ; 2 - МТ; 3 - A;
4 - АТ; 5 - АД0; ACT; 6 - АД31Т1; 7 - АД31Т; 8 - Ст3
Рисунок 21
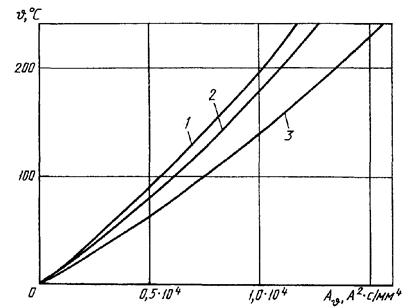
Кривые для определения температуры нагрева проводов
при КЗ
Материалы
проводов: 1 - сплавы АЖ и АЖКП; 2 - сплавы АН и АНКП; 3 - алюминий
марок А, АКП, АпКП и сталеалюминий марок АС, АСКП, АСКС, АСК, АпС, АпСКС, АпСК
Рисунок 22
С этой целью необходимо:
1) на рисунке 21 выбрать кривую,
соответствующую материалу проводника, и по этой кривой, исходя из начальной
температуры проводника Jн,
определить значение функции АJн, ![]() с2/мм4;
с2/мм4;
2) в соответствии с указаниями пп. 3.1.5-3.1.8
определить значение интеграла Джоуля Bтер;
3) найти значение функции АJк , соответствующее конечной температуре нагрева
проводника Jк
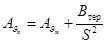 , (54)
, (54)
где S - площадь
поперечного сечения проводника, мм2.
При расчете температуры нагрева сталеалюминиевых
проводов в формулу (54) следует вводить площадь поперечного сечения
алюминиевой части провода;
4) по найденному значению функции AJк , используя выбранную кривую на рисунке 21,
определить конечную температуру нагрева проводника Jк и
сравнить ее с предельно допустимой температурой. Предельно допустимые
температуры нагрева проводника при КЗ приведены в таблице 6.
Таблица 6
- Предельно допустимые температуры нагрева проводников при КЗ
|
Вид проводников
|
Jдоп, °С
|
|
1 Шины алюминиевые
|
200
|
|
2 Шины медные
|
300
|
|
3 Шины стальные, не имеющие непосредственного соединения с аппаратами
|
400
|
|
4 Шины стальные с непосредственным присоединением к аппаратам
|
300
|
|
5 Кабели с бумажной пропитанной изоляцией на напряжение, кВ:
до 10
|
200
|
|
20-35
|
130
|
|
110-220
|
125
|
|
6 Кабели и изолированные провода с медными и алюминиевыми жилами и
изоляцией из:
поливинилхлорида
|
160
|
|
резины
|
150
|
|
резины повышенной теплостойкости
|
250
|
|
полиэтилена (номинальное напряжение кабеля до 35 кВ)
|
130
|
|
вулканизированного
полиэтилена (номинальное напряжение кабеля до 35 кВ)
|
250
|
|
7 Медные неизолированные провода при тяжениях, Н/мм2:
менее 20
|
250
|
|
20 и более
|
200
|
|
8 Алюминиевые неизолированные провода при тяжениях, Н/мм2:
менее 10
|
200
|
|
10 и более
|
160
|
|
9 Алюминиевая часть сталеалюминиевых проводов
|
200
|
3.3.3 Если определяющим
условием при выборе сечения проводника является его термическая стойкость при
КЗ, то следует определить минимальное сечение проводника по условию термической
стойкости (Sтер.min) в
миллиметрах в квадрате, используя выражение
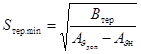 , (55)
, (55)
где AJдоп -
значение функции AJ, соответствующее
предельно допустимой температуре нагрева проводника при КЗ (см. таблицу 6);
АJн - значение этой функции, соответствующее температуре
проводника до КЗ.
Термическая стойкость проводника
обеспечивается, если площадь сечения (S) в
миллиметрах в квадрате удовлетворяет неравенству:
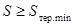 .
.
3.3.4 Если нагрузка проводника до КЗ
близка к продолжительно допустимой, то минимальное сечение проводника,
отвечающее требованию термической стойкости при КЗ, определяют по формуле
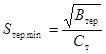 , (56)
, (56)
где 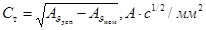 ;
;
АJном - значение функции А при продолжительно допустимой
температуре проводника.
Значения параметра Ст в
таблице 9.
Таблица 7
- Значения параметров Ст жестких шин
|
Система
легирования
|
Материал
проводника или марка сплава
|
Значение
Ст, ![]() с1/2 мм2, при
начальной температуре, oС с1/2 мм2, при
начальной температуре, oС
|
|
70
|
90
|
120
|
|
-
|
Медь
|
170
|
.
. .
|
.
. .
|
|
Аl
|
АДО
|
90
|
81
|
68
|
|
АД1Н
|
91
|
82
|
69
|
|
АД0М,
АД1М
|
92
|
83
|
70
|
|
Al-Mg-Si
|
АД31Т1
|
85
|
77
|
64
|
|
АД31Т
|
82
|
74
|
62
|
|
АДЗЗТ1
|
77
|
71
|
59
|
|
АДЗЗТ
|
74
|
67
|
57
|
|
АВТ1
|
73
|
66
|
55
|
|
АВТ
|
71
|
63
|
53
|
|
Al-Zn-Mg
|
1911
|
71
|
63
|
53
|
|
1915, 1915Т
|
66
|
60
|
51
|
|
Al-Mg-Mn
|
АМг5
|
63
|
57
|
48
|
|
-
|
Сталь
при Jдоп = 400 °С
|
70
|
.
. .
|
.
. .
|
|
Сталь
при Jдоп= 300 °С
|
60
|
.
. .
|
.
. .
|
Таблица 8
- Значения параметра Ст кабелей
|
Характеристика
кабелей
|
Значение
Ст,![]() с1/2/мм2 с1/2/мм2
|
|
1 Кабели до 10 кВ:
с медными жилами
|
140
|
|
с алюминиевыми жилами
|
90
|
|
2 Кабели 20-35 кВ:
с медными жилами
|
105
|
|
с алюминиевыми жилами
|
70
|
|
3 Кабели и изолированные провода с полихлорвиниловой или резиновой
изоляцией:
с медными жилами
|
120
|
|
с алюминиевыми жилами
|
75
|
|
4 Кабели и изолированные провода с полиэтиленовой изоляцией:
с медными жилами
|
103
|
|
с алюминиевыми жилами
|
65
|
Таблица 9
- Значения параметра Ст проводов
|
Материал провода
|
Марка
провода
|
Значения
параметра Ст, А×с/мм2,
при допустимых температурах нагрева проводов при КЗ, °С
|
|
160
|
200
|
250
|
|
1 Медь
|
М
|
-
|
142
|
162
|
|
2 Алюминий
|
А,
АКП, Ал, АпКП
|
76
|
90
|
-
|
|
3 Алюминиевый
сплав
|
АН,
АНКП,
|
69
|
81
|
-
|
|
АЖ,
АЖКП
|
66
|
77
|
-
|
|
4 Алюминий -
сталь
|
АСК,
АпС, АСКС, АпСКС, АпСК, АС, АСКП
|
76
|
90
|
-
|
3.3.5 Допускается проверку
проводников на термическую стойкость при КЗ проводить путем сравнения
термически эквивалентной плотности тока КЗ (Jтер.эк)в амперах на квадратный миллиметр
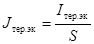 (57)
(57)
с допустимой в течение расчетного времени КЗ
плотностью тока (Jтер.доп) в
амперах на квадратный миллиметр
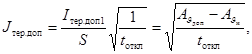 (58)
(58)
где Iтер.доп1 -
допустимый ток односекундного КЗ, А; его значения для кабелей даны в нормативных
документах.
Проводник удовлетворяет условию
термической стойкости при КЗ, если выполняется соотношение
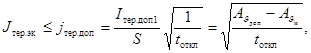 (59)
(59)
3.3.6 Если нагрузка проводника до КЗ
близка к продолжительно допустимой, то допускается проверку проводника на
термическую стойкость при КЗ проводить, используя соотношение
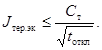 (60)
(60)
3.4.1 Для проверки силовых кабелей на
невозгораемость при КЗ следует в соответствии с п. 3.3.2 определить конечную
температуру нагрева их жил Jк при расчетной продолжительности КЗ (см. п. 1.1.5)
и сравнить ее с предельной температурой невозгораемости Jнв
Невозгораемость кабеля обеспечивается,
если выполняется условие
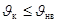 . (61)
. (61)
Предельная температура невозгораемости
кабелей 6 кВ с пропитанной бумажной изоляцией равна 400 °С для бронированных и
350 °С - для небронированных кабелей.
(рекомендуемое)
1.1 Максимальное возможное тяжение в
проводниках (Fmax f) в ньютонах следует определять по формуле
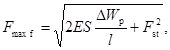
где S - площадь
поперечного сечения проводника, м2;
DWр - расчетная энергия;
DWp = DWк при DWк / Mgl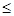 2;
2;
DWp=2Mgl
при DWк / Mgl>2,
где DWк - энергия, накопленная проводником одного пролета за
расчетное время КЗ, Дж;
l - длина проводника в пролете, м;
Fst - тяжение в проводнике до
КЗ, равное 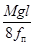 ;
;
Mgl - максимально возможная расчетная потенциальная
энергия проводника;
M - масса
проводника в пролете, кг;
g - ускорение
свободного падения, м/с2;
fп - провес проводника в пролете, м;
L - расстояние
от прямой, соединяющей точки крепления проводов на соседних опорах, до центра
масс провода в пролете, м, причем
L=2fп/3.
Модуль упругости (Е) проводника,
свитого из пучка тонких проволок, как при наличии упрочняющего стального
провода, так и без него, следует принимать меньшим, чем модуль упругости
материала проводника из-за повышенной растяжимости витого проводника при
нагружении. Его значение необходимо определять опытным путем.
1.2 Максимальное смещение провода (Sотк) в метрах следует определять по формулам:
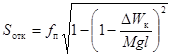 при
при 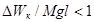 ;
;
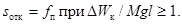
При кратковременном КЗ энергию,
накопленную проводником (DWк) в джоулях, следует вычислять по формуле
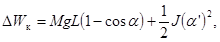
где a и a’ - угол отклонения провода и его первая производная по времени в
момент отключения КЗ;
J - момент инерции провода относительно оси, проходящей
через опоры провода, м4.
Кривые зависимости относительных
параметров проводника (DWк
/ MgL) от относительной продолжительности КЗ (t) относительных нагрузок на провод 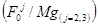 и относительных размеров (a/L)
при двух- и трехфазном КЗ приведены
соответственно на рисунках 23 и 24. При этом относительную
продолжительность КЗ следует определять как
и относительных размеров (a/L)
при двух- и трехфазном КЗ приведены
соответственно на рисунках 23 и 24. При этом относительную
продолжительность КЗ следует определять как
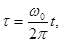
где t -
расчетная продолжительность КЗ, с;
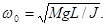
Нагрузки (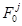 ) в ньютонах следует
определять для различных видов КЗ (j = 2,3):
) в ньютонах следует
определять для различных видов КЗ (j = 2,3):
- для двухфазного КЗ
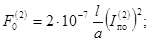
- для трехфазного КЗ
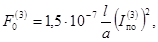
где 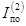 и
и 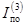 - начальные действующие
значения периодической составляющей токов соответственно двух- и трехфазного
КЗ, А.
- начальные действующие
значения периодической составляющей токов соответственно двух- и трехфазного
КЗ, А.
1.3. При относительной продолжительности
КЗ t > 0,6 энергию, накопленную проводником (DWк ) в
джоулях, следует определять в зависимости от вида КЗ:
- при двухфазном КЗ
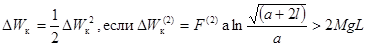 ;
;
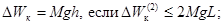
- при трехфазном КЗ
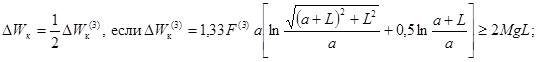
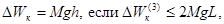
где h - максимальная
высота подъема центра масс провода во время КЗ, определяемая из соотношения h/a, м.
Параметры h/a для
случаев двух- и трехфазного КЗ следует определять по кривым, приведенным
соответственно на рисунках 25 и 26.
Характеристики ![]() при двухфазном КЗ
при двухфазном КЗ
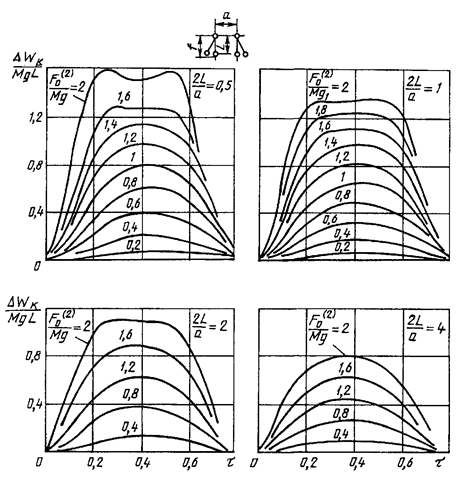
Рисунок 23
Характеристики ![]() при трехфазном
КЗ
при трехфазном
КЗ
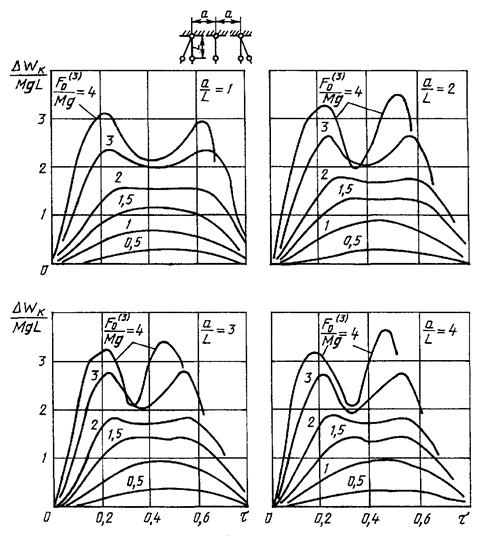
Рисунок 24
Характеристики 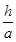 при
двухфазном КЗ
при
двухфазном КЗ
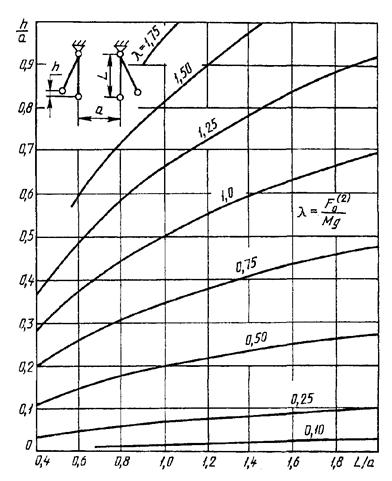
Рисунок 25
Характеристики - при
трехфазном КЗ
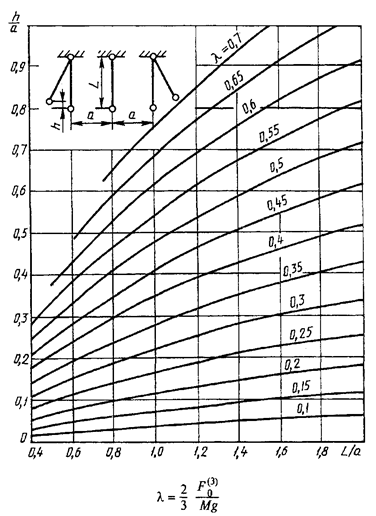
Рисунок 26
Допустимое сближение фаз оценивают по
следующему условию
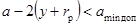 ,
,
где у - максимальное отклонение провода, м;
а - расстояние между токопроводами соседних фаз, м;
rр- радиус
расщепления фазы, м;
amin доп - наименьшее
допустимое расстояние между фазами, м.
Максимальное отклонение провода при
двухфазном КЗ определяют по выражению
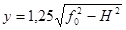 ,
,
где fo - стрела провеса провода, м;
H - высота
расположения провода относительно точки подвеса в момент его максимального
отклонения, м, которая равна
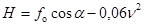 ,
,
где а - угол отклонения провода фазы к моменту
отключения КЗ, рад;
n - скорость движения центра масс провода к моменту
отключения КЗ, м/с.
Угол а определяют по формуле
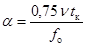 ,
,
где tк - расчетная продолжительность КЗ, с.
Скорость n определяют
по формуле
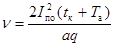 ,
,
где Iпо -
начальное действующее значение периодической составляющей тока КЗ, кА;
Та - постоянная времени затухания апериодической составляющей
тока КЗ, с;
q - приведенная
нагрузка на фазу, Н/м, которая равна q - рК, где р - погонный вес фазы, Н/м;
К - коэффициент нагрузки, учитывающий
влияние натяжных гирлянд изоляторов и спусков. Например, для пролета воздушной
линии К = 1, для пролета наружной электроустановки с двумя натяжными
гирляндами
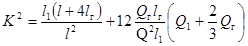 ,
,
где
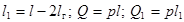 .
.
Если H<0, то
принимать H=0
(рекомендуемое)
Таблица 10 - Расчетные выражения для определения коэффициента
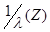
|
Норма расчетной схемы в таблице 2
|
Расчетная
формула для определения коэффициента 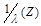
|
Норма
расчетной схемы в таблице 2
|
Расчетная
формула для определения коэффициента 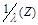
|
|
1
|
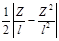
|
5
|
а)
Для крайнего пролета
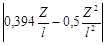
б)
Для второго пролета
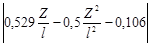
в)
для среднего пролета
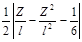
|
|
2
|
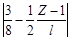
|
|
3
|
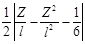
|
|
4
|
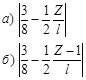
|
(рекомендуемое)
Наибольшее напряжение в материале шин и
максимальную нагрузку на изоляторы при повторном включении на КЗ определяют по
формулам:
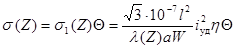 ;
;
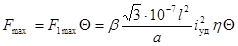 ,
,
где s1(Z) и F1max - наибольшее
напряжение и нагрузка при первом КЗ;
Q - коэффициент превышения напряжения и нагрузки при
повторном КЗ.
Коэффициент превышения Q определяют по кривым рисунка 27а в зависимости от декремента
затухания d. Номер расчетной кривой на рисунке 27а
определяют в зависимости от продолжительности бестоковой паузы tб.п и частоты собственных
колебаний шины f1,
используя рисунок 27б. Если точка с координатами tб.п и f1 лежит в зоне,
ограниченной осями координат и кривой I, то
коэффициент Q определяют по кривой 1 рисунок 27а.
Если эта точка лежит в зоне, ограниченной кривыми I и II, то Q определяют по кривой 2 и т.д. Следует отметить, что расчетные
коэффициенты Q получены при наиболее неблагоприятных условиях
коммутаций, которые приводят при первом КЗ, в бестоковую паузу и повторном
включении на КЗ к наибольшим напряжениям в материале шин и нагрузкам на
изоляторы и таким образом обеспечивают оценку электродинамической стойкости
ошиновки.
К определению коэффициента превышения Q в зависимости от d, tб.п, f1
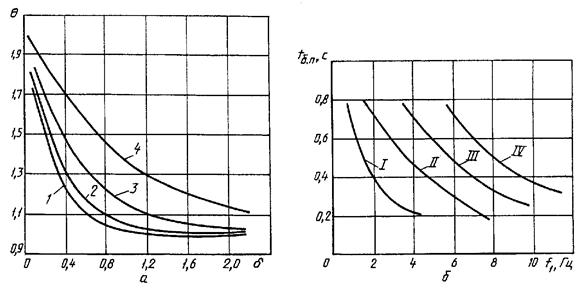
Рисунок 27
(рекомендуемое)
Пример 1. Проверить электродинамическую стойкость трехфазной
шинной конструкции, изоляторы которой обладают высокой жесткостью, при действии
тока КЗ ![]() =
155 rА.
=
155 rА.
Шины выполнены из алюминиевого сплава
марки АД31T1, имеют прямоугольное сечение (60 ´ 6) мм2, четыре пролета, расположены в
одной плоскости и их параметры:
l = 1,2 м; а= 0,6 м; т = 0,972 кг/м;
Е = 7 1010 Па; sдоп = 137,2 МПа.
Согласно таблице 4
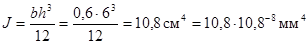 ;
;
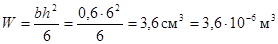 .
.
Частота собственных колебаний
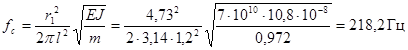 ,
,
где r1 = 4,73
соответствует расчетной схеме 5, таблицы 2.
В соответствии с рисунком 5
коэффициент динамической нагрузки равен h = 1,1.
Максимальное напряжение в шинах, определяемое по формуле (15),
равно
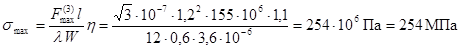 ,
,
где 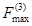 определено по формуле (2),
коэффициент l - из таблицы 2.
определено по формуле (2),
коэффициент l - из таблицы 2.
Поскольку smax = 254 МПа > sдоп= 137,2 МПа, то шины не удовлетворяют условию
электродинамической стойкости. Для снижения максимального напряжения в
материале шин необходимо уменьшить длину пролета. Наибольшая допустимая длина
пролета
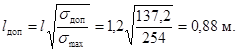
Примем длину пролета l
= 0,8 м.
В этом случае f1 =491 Гц; h = 1,04 и
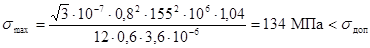 .
.
Максимальную нагрузку на изолятор
определяем по формуле (2):
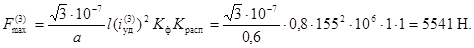
Выбираем изоляторы типа ИОР-10-16,00
УХЛЗ. Они удовлетворяют условию электродинамической стойкости (29), так как
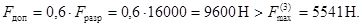
Таким образом, шинная конструкция при
уменьшении длины пролета до 0,8 м отвечает требованиям электродинамической
стойкости.
Пример 2. Проверить электродинамическую стойкость трехфазной
шинной конструкции в цепи генератора, шины которой состоят из двух элементов
корытного профиля при ![]() = 120 кА.
= 120 кА.
Алюминиевые шины (марки АДО) сечением 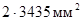 расположены
в горизонтальной плоскости и имеют следующие параметры: l
= 2 м; а = 0,75 м; mэл = 9,27
кг/м; Е =
расположены
в горизонтальной плоскости и имеют следующие параметры: l
= 2 м; а = 0,75 м; mэл = 9,27
кг/м; Е = ![]() Па; sдоп = 41 МПа; aэл = 0,2 м; lэл = 1 м;
Па; sдоп = 41 МПа; aэл = 0,2 м; lэл = 1 м; 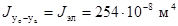 ;
; 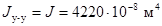 ;
; 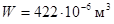 ;
; 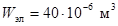 .
.
Частоты собственных колебаний шины и
элемента шины, определяемые по формулам (22) и (24), равны
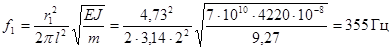 ;
;
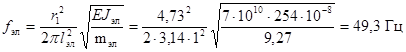 .
.
Для полученных значений f1 и f1эл, h и hэл равны
1,0 (рисунок 5).
Максимальные напряжения в материале шин, которые
обусловлены взаимодействием токов разных фаз и токов элементов одной фазы в
соответствии с формулами (15) и (22) равны
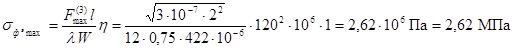 ;
;
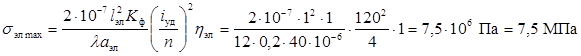 .
.
Суммарное напряжение в материале шины
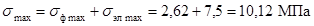 .
.
Шины удовлетворяют условию
электродинамической стойкости, так как
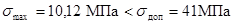 .
.
Максимальная нагрузка на изолятор,
определяемая по формуле (2), равна
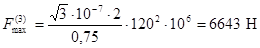 .
.
Выбираем изолятор типа ИО-10-20,00 УЗ.
Разрушающая нагрузка для этого изолятора
составляет Fразр =
20000 Н, высота Hиз = 34
мм. Изолятор имеет внутреннее крепление арматуры (рисунок 3а), поэтому hц = аэл/2 = 0,1 м. Согласно (8)
допустимая нагрузка при изгибе изолятора равна
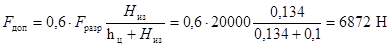 .
.
Расчетная максимальная нагрузка на
изоляторы не превышает допустимую
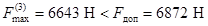 ,
,
поэтому изолятор типа ИО-10-20,00 УЗ удовлетворяет
условиям электродинамической стойкости.
Пример 3. Проверить электродинамическую стойкость шинной
конструкции наружной электроустановки напряжением 110 кВ при iуд = 50 кА. Трубчатые шины квадратного сечения выполнены из
алюминиевого сплава АД31Т и расположены в одной плоскости. Высота шины Н = 125
мм, толщина t = 8 мм,
погонная масса т = 8,96 кг/м. Длина пролета l = 5,0 м;
расстояние между фазами а = 1,0 м. Допустимое напряжение в материале
шины sдоп = 89
МПа, модуль упругости E =![]() Па.
Изоляторы типа ИОС-110-600 имеют высоту Hиз = 1100 мм, расстояние от головки изолятора до центра
тяжести шины hц = 80 мм,
высоту арматуры нижнего фланца изолятора Hарм = 100 мм.
Па.
Изоляторы типа ИОС-110-600 имеют высоту Hиз = 1100 мм, расстояние от головки изолятора до центра
тяжести шины hц = 80 мм,
высоту арматуры нижнего фланца изолятора Hарм = 100 мм.
Жесткость изолятора Сиз
= 1100 кН/м, частота собственных колебаний fиз = 28 Гц.
Момент инерции и момент сопротивления
шины в соответствии с формулами таблицы 4 составляют
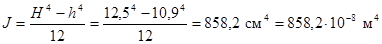 ;
;
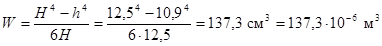 ;
;
где h
= H - 2t
= 12,5 - 1,6 = 10,9 см.
Допустимая нагрузка на изолятор
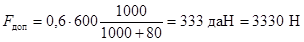 ,
,
где H = Hиз - Hарм = 1100 - 100 = 1000 мм.
Значения жесткости и частоты колебаний
опоры допустимо принять равными жесткости и частоте колебаний изолятора, так
как изоляторы шинной конструкции установлены на весьма жестком основании.
Приведенная масса в соответствии с формулой (28)
равна
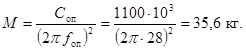
Необходимые для определения параметра
основной частоты величины соответственно равны
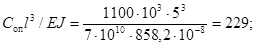
![]()
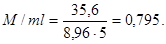
По кривым рисунка 6 параметры частоты r1 = 3,3, поэтому
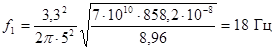 .
.
По кривой рисунка 5 h = 0,90.
Максимальное напряжение в материале шины
и нагрузка на изоляторы в соответствии с (15) и (2)
составляют
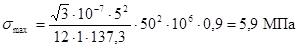 ;
;
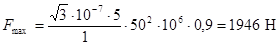 , т.е.
, т.е.
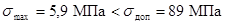 и
и
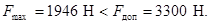
Шинная конструкция удовлетворяет условиям
электродинамической стойкости.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1 РАЗРАБОТАН Подкомитетом ПК-2 Технического комитета
по стандартизации ТК 117 ВНЕСЕН Госстандартом Российской Федерации
2 Принят Межгосударственным советом по стандартизации,
метрологии и сертификации (протокол № 7 от 26 апреля 1995 г.)
За принятие проголосовали:
|
Наименование
государства
|
Наименование
национального органа по стандартизации
|
|
Азербайджанская
Республика
|
Азгосстандарт
|
|
Республика
Армения
|
Армгосстандарт
|
|
Республика
Беларусь
|
Госстандарт Республики Беларусь
|
|
Республика
Казахстан
|
Госстандарт Республики
Казахстан
|
|
Кыргызская
Республика
|
Кыргызстандарт
|
|
Республика
Молдова
|
Молдовастандарт
|
|
Российская
Федерация
|
Госстандарт России
|
|
Республика
Таджикистан
|
Таджикстандарт
|
|
Туркменистан
|
Главгосслужба
«Туркменстандартлары»
|
|
Республика
Узбекистан
|
Узгосстандарт
|
3 Настоящий стандарт представляет собой полный
аутентичный текст ГОСТ
Р 50254-92 «короткие замыкания в электроустановках. Методы расчета
электродинамического и термического действия тока короткого замыкания»
4 Постановлением комитета Российской Федерации по
стандартизации, метрологии и сертификации от 12 марта 1996 г. № 164 межгосударственный
стандарт ГОСТ 30323-95 введен в действие непосредственно в качестве
государственного стандарта Российской Федерации с 1 июля 1996 г.
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Август 2004 г.
Новости
Библиотека
Soft по ОТ и ПБ
Консультации
Агрегатор
Услуги
Форум
Золотой фонд
ССОТ
CHAT-OT


.webp)