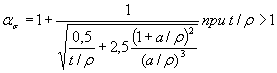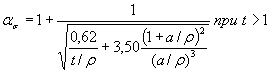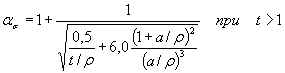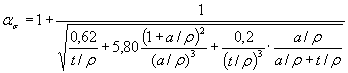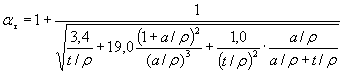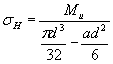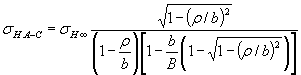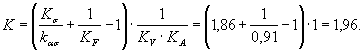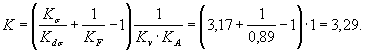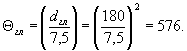| МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ |
| Расчеты и испытания на прочность МЕТОДЫ РАСЧЕТА ХАРАКТЕРИСТИК СОПРОТИВЛЕНИЯ УСТАЛОСТИ Strength calculation and testing.
Methods of fatigue strength behaviour calculation | ГОСТ
25.504-82 |
Дата введения 01.07.83
Настоящий стандартустанавливает методы расчета следующих характеристик сопротивления усталостидеталей машин и элементов конструкций, изготовленных из сталей, в много- ималоцикловой упругой и упругопластической области:
- медианных значений пределоввыносливости на базе 107 циклов;
- пределов выносливости длязаданной вероятности разрушения на базе 107 циклов;
- коэффициента вариациипределов выносливости;
- показателя наклона левойветви кривой усталости в двойных логарифмических координатах
- абсциссы точки перелома кривойусталости;
- коэффициентачувствительности к асимметрии цикла напряжений;
- предельных амплитуд приасимметричных циклах нагружения;
- параметров уравнения кривоймалоцикловой усталости (в пределах до 105 циклов) при: растяжении -сжатии, изгибе и кручении,
- симметричных и асимметричных циклахнапряжений или деформаций, изменяющихся по простому периодическому закону спостоянными параметрами,
абсолютных размерах поперечного сечениядетали до 300 мм,
наличии и отсутствии концентрациинапряжений,
температуре от минус 40°С до плюс 100°С,
наличии и отсутствии агрессивной среды,
частоте нагружения в пределах 1 - 300 Гц.
Стандарт не распространяется на методырасчета характеристик сопротивления усталосп сварных конструкций и ихэлементов.
Область применения стандартаограничивается случаями, для которых в тексте стандарта приложений имеются всеисходные и справочные данные.
Выбор требуемой номенклатурыхарактеристик сопротивления много- и малоцикловой усталости определяется вкаждом конкретном случае задачами и методом расчета по действующим отрасляхнормативно-техническим документам.
Термины, определения и обозначения,применяемые в стандарте, - по ГОСТ23207.
Обозначения, применяемые в стандарте,приведены в приложении1.
Размерность напряжений - МПа,геометрических размеров - мм.
Настоящий стандарт унифицирован состандартами ГДР ТГЛ 19340/03 и ТГЛ 19340/04.
(Измененная редакция, Изм. № 1).
СОДЕРЖАНИЕ
| 1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ МАШИН И ЭЛЕМЕНТОВ КОНСТРУКЦИЙ 1.1. Определение медианных значений пределов выносливости 1.2. Определение эффективных коэффициентов концентрации напряжений Кσ, Кτ и отношений Kσ/Kdσ, Kτ/Kdτ 1.3. Определение коэффициентов К1 1.4. Определение теоретических коэффициентов концентрации напряжений ασ, ατ 1.5. Определение значения относительного критерия подобия усталостного разрушения 1.6. Определение параметра L 1.7. Определение относительного градиента первого главного или касательного напряжений 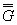 , ,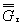 1.8. Определение коэффициентов чувствительности металла к концентрации напряжений и масштабному фактору vσ и vτ 1.9. Определение коэффициентов влияния шероховатости поверхности КFσ, КFτ 1.10. Определение коэффициента Kкор 1.11. Определение коэффициента влияния поверхностного упрочнения Kv и коэффициента анизотропии KА 2. ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ МАШИН И ЭЛЕМЕНТОВ КОНСТРУКЦИЙ ДЛЯ ЗАДАННОЙ ВЕРОЯТНОСТИ РАЗРУШЕНИЯ [σ-1Д]р 3. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ВАРИАЦИИ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ МАШИН И ЭЛЕМЕНТОВ КОНСТРУКЦИЙ 3.2. Определение коэффициентов вариации 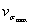 3.3. Определение коэффициентов вариации 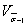 3.4. Определение коэффициентов вариации 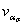 4. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ КРИВЫХ УСТАЛОСТИ m И NG И КОЭФФИЦИЕНТОВ ЧУВСТВИТЕЛЬНОСТИ К АСИММЕТРИИ ЦИКЛА НАПРЯЖЕНИЙ Ψσ И Ψτ 5. ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ ХАРАКТЕРИСТИК СОПРОТИВЛЕНИЯ МАЛОЦИКЛОВОЙ УСТАЛОСТИ 5.3. Определение напряжений и деформаций 5.4. Определение диаграмм статического и циклического деформирования 5.5. Определение располагаемой пластичности материала 5.6. Определение кривой малоцикловой усталости ПРИЛОЖЕНИЕ 1 Обязательное ОБОЗНАЧЕНИЯ, ПРИМЕНЯЕМЫЕ В СТАНДАРТЕ ПРИЛОЖЕНИЕ 2 Обязательное ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНЫХ КОЭФФИЦИЕНТОВ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ КσКτ ОТНОШЕНИЙ 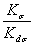 , , 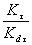 , КОЭФФИЦИЕНТОВ n, q, К1, И К3 , КОЭФФИЦИЕНТОВ n, q, К1, И К3 ПРИЛОЖЕНИЕ 3 Обязательное ОПРЕДЕЛЕНИЕ ТЕОРЕТИЧЕСКИХ КОЭФФИЦИЕНТОВ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ ασ, ατ ПРИЛОЖЕНИЕ 4 Обязательное ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИИ F (Θ , v), ПАРАМЕТРА L, КОЭФФИЦИЕНТА ВЛИЯНИЯ ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ КF И КОЭФФИЦИЕНТА Ккор ПРИЛОЖЕНИЕ 5 Рекомендуемое ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ВЛИЯНИЯ ПОВЕРХНОСТНОГО УПРОЧНЕНИЯ Kv ПРИЛОЖЕНИЕ 6 Справочное ПРИМЕРЫ РАСЧЕТА ХАРАКТЕРИСТИК СОПРОТИВЛЕНИЯ УСТАЛОСТИ ДЕТАЛЕЙ МАШИН ПРИЛОЖЕНИЕ 7 Справочное ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАНДАРТА БИБЛИОГРАФИЯ ИНФОРМАЦИОННЫЕ ДАННЫЕ |
Медианные значения пределов выносливостидеталей машины в номинальных напряжениях 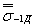 (соответствующиевероятности разрушения Р = 50%) определяют с учетом коэффициента снижения предела выносливости К по формулам:
(соответствующиевероятности разрушения Р = 50%) определяют с учетом коэффициента снижения предела выносливости К по формулам:
- при растяжении - сжатии илиизгибе
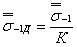 , (1)
, (1)
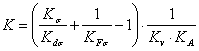 , (2)
, (2)
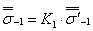 , (3)
, (3)
| где 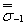 | - медианное значение предела выносливости на совокупности всех плавок металла данной марки гладких лабораторных образцов диаметром d0 = 7,5 мм, изготовленных из заготовок диаметром d, равным абсолютному размеру рассчитываемой детали; |
| 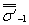
| - медианное значение предела выносливости на совокупности всех плавок металла данной марки гладких лабораторных образцов диаметром d0 = 7,5 мм, изготовленных из заготовок размерами 10-20 мм; |
| k1 | - коэффициент, учитывающий снижение механических свойств металла (σB , σT , σ-1) с ростом размеров заготовок (п. 1.3); |
- при кручении
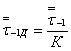 , (4)
, (4)
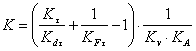 , (5)
, (5)
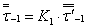 . (6)
. (6)
Медианные значения пределов выносливостидеталей 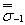 ,
, 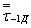 полученные поформулам (1) и (4) для Р = 50%, используют для оценки пределов выносливости деталей при любой заданнойвероятности разрушения (разд. 2и 3).
полученные поформулам (1) и (4) для Р = 50%, используют для оценки пределов выносливости деталей при любой заданнойвероятности разрушения (разд. 2и 3).
Примечания:
1. При наличии коррозионных воздействий в формулы (2) и (5)вместо KFследуетподставлять значения Kкор
2. При отсутствии экспериментальныхданных ориентировочно величины 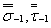 , допускается оценивать на основе соотношений:
, допускается оценивать на основе соотношений:
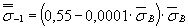 , (7)
, (7)
где 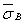 - среднее значениепредела прочности стали данной марки, определенное на образцах, изготовленныхиз заготовок диаметром d, равным абсолютному размерурассчитываемой детали, МПа;
- среднее значениепредела прочности стали данной марки, определенное на образцах, изготовленныхиз заготовок диаметром d, равным абсолютному размерурассчитываемой детали, МПа;
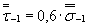 . (8)
. (8)
1.2.1.Коэффициенты Кσ, Кτ и отношения Kσ/Kdσ, Kτ/Kdτ определяют поэкспериментальным данным или путем расчета.
1.2.2. Определение Кσ , Кτ, Kσ/Kdσ и Kτ/Kdτ - по экспериментальным данным.
Коэффициенты Кσ, Кτ могут определяться экспериментальнона геометрически подобных образцах диаметром d или толщиной h поперечного сечения не менее 40 мм, если d или h рассчитываемойдетали превышают это значение. Если d или h рассчитываемойдетали меньше 40 мм, то при экспериментальном определении Кσ, Кτ целесообразно вестииспытания на натурных деталях или моделях тех же поперечных размеров.
Для ряда деталей экспериментальнополученные значения Кσ, Кτ и Kσ/Kdσ, Kτ/Kdτ приведены в приложении 2 (черт. 1-7, 13-16).
Значения (Kσ/Kdσ)0для валов с напрессованными деталями (при наличиикоррозии трения) при изгибе представлены на черт. 1 приложения 2.
При σB > 500 МПа и ρ < 30 МПа следует учитывать соответствующие поправочныекоэффициенты 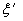 и
и 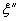 (черт. 2, 3) и определять значения Kσ/Kdσ по формуле
(черт. 2, 3) и определять значения Kσ/Kdσ по формуле
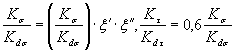 . (10)*
. (10)*
(Измененнаяредакция, Изм. № 1).
*Формула 9. (Исключена, Изм. № 1).
1.2.3. Определение Кσ, Кτи Kσ/Kdσ, Kσ/Kdσ методом расчета
1.2.3.1. КоэффициентыКσ, Кτ, Kdτ., Kdσи отношение 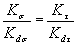 в случае отсутствияпрямых экспериментальных данных могут быть вычислены по формулам (при известныхзначениях vσ , vτ , α и G):
в случае отсутствияпрямых экспериментальных данных могут быть вычислены по формулам (при известныхзначениях vσ , vτ , α и G):
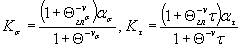 , (11)
, (11)
 ,
,
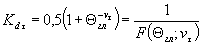 , (12)
, (12)
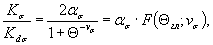
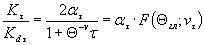 , (12а)
, (12а)
где 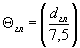 - значениеотносительного критерия подобия усталостного разрушения для гладкого (безконцентрации напряжений) образца диаметром dгл, мм.
- значениеотносительного критерия подобия усталостного разрушения для гладкого (безконцентрации напряжений) образца диаметром dгл, мм.
Определение относительного критерияподобия усталостного разрушения Θ, величин vσ, vτ и функции F(Θ , v) приведенов пп. 1.5и 1.8.
1.2.3.2. Если известны тольковеличины ασ, ατи 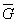 , то Кσ или Кτ вычисляют приближенно по формулам:
, то Кσ или Кτ вычисляют приближенно по формулам:
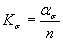 ; (13)
; (13)
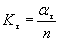 , (14)
, (14)
Коэффициент n вычисляют по формуле
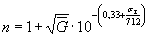 (15)
(15)
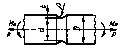
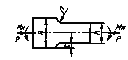
или по черт. 14приложения 2 в зависимости от значений относительного градиента напряжений 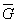 (мм-1),вычисленного по формулам, приведенным в табл. 1, и предела текучести σт (МПа).
(мм-1),вычисленного по формулам, приведенным в табл. 1, и предела текучести σт (МПа).
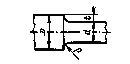
Таблица 1
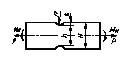
| Деталь | Формулы для вычисления 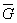 , , 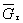 |
| Изгиб | Растяжение- сжатие | Кручение |
| 
| 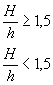
| 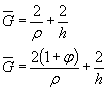
| 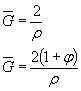
| - |
| 
| 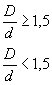
| 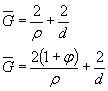
| 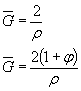
| 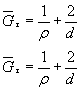
|
| 
| 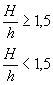
| 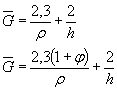
| 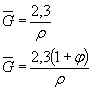
| - |
| 
| 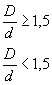
| 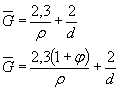
| 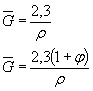
| 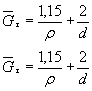
|
| 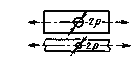
| | - | 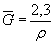
| - |
Примечание.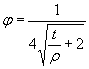
1.2.3.3.В приближенных расчетах значения Кσ и Кτ вычисляют по формулам:
Кσ =1 + q(ασ-1), (18)*
Кτ =1 + q(ατ-1), (19)
где значения коэффициентовчувствительности металла к концентрации напряжений q определяют по черт. 15приложения 2.
1.2.3.1.-1.3. (Измененная редакция, Изм. № 1).
1.3.1.Коэффициент К1 длялегированных сталей определяют по черт. 16 приложения 2 или по формуле
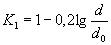 для d ≤ 150 мм, (20)
для d ≤ 150 мм, (20)
где d0 = 7,5 мм - диаметр гладкого лабораторного образца;
K1 = 0,74 для d >150 мм.
Для углеродистых сталей К1 = 1.
1.3.2, 1.3.3. (Исключены,Изм. № 1).
*Формулы 16 и 17. (Исключены, Изм. № 1).
1.4.1. Коэффициенты ασ, ατ определяют потеоретическим решениям или на основе измерений с помощьюполяризационно-оптического метода, тензометрирования и т.п. (приложение 3, черт. 1-47).
1.4.2. Для определениятеоретических коэффициентов концентрации напряжений в деталях, изображенных втабл. 2, могут быть использованы также номограммы, приведенные на черт. 48 и 49 приложения 3.
Примечания:
1. Пример использования номограмм для элементов сдвусторонней внешней выточкой при изгибе.
Дано: ρ = 2,5мм; t = 15 мм; а = 95мм.
Находим 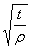 = 2,45;
= 2,45; 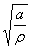 = 6,16.
= 6,16.
Как вытекает из табл. 2, для 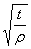 нужно воспользоватьсярядом чисел b, а для
нужно воспользоватьсярядом чисел b, а для 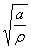 - кривой 2. По черт. 48 от абсциссы
- кривой 2. По черт. 48 от абсциссы 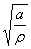 =6,16 начинаемдвигаться по вертикали вверх до пересечения с кривой 2. Затем налево проводимгоризонтальную линию до пересечения с осью ординат. Точку пересечения соединяемс точкой
=6,16 начинаемдвигаться по вертикали вверх до пересечения с кривой 2. Затем налево проводимгоризонтальную линию до пересечения с осью ординат. Точку пересечения соединяемс точкой 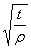 =2,45, находящейся нагоризонтальной оси, при этом отсчет производим по ряду чисел b. Прямая касается круга, указывающего коэффициент концентрации ασ = 4,28.
=2,45, находящейся нагоризонтальной оси, при этом отсчет производим по ряду чисел b. Прямая касается круга, указывающего коэффициент концентрации ασ = 4,28.
2. Пример использования номограммы для элементов с внешнейвыточкой и осевым отверстием при изгибе.
Дано: ρ = 4 мм; а = 13 мм; t = 36 мм; r = 25 мм.
Находим 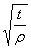 = 3,
= 3, 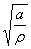 = 1,80,
= 1,80, 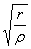 =2,50.
=2,50.
Как указано в примере 1 при 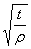 (ряд чисел b) и
(ряд чисел b) и 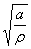 (кривая 5) на черт. 48 находим
(кривая 5) на черт. 48 находим 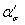 = 3,60. Это будет теоретический коэффициентконцентрации напряжений при большом осевом отверстии
= 3,60. Это будет теоретический коэффициентконцентрации напряжений при большом осевом отверстии 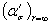 .
.
Теперь переходим к черт. 49 и смещаемся вверх по вертикали при значении 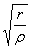 = 2,50 до пересеченияс кривой 2, затем налево по горизонтали до пересечения с осью. Точкупересечения соединяем с прямой
= 2,50 до пересеченияс кривой 2, затем налево по горизонтали до пересечения с осью. Точкупересечения соединяем с прямой 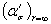 = 3,60, лежащей на другой оси. Круг,которого касается эта прямая, дает ασ= 2,08.
= 3,60, лежащей на другой оси. Круг,которого касается эта прямая, дает ασ= 2,08.
Таблица 2
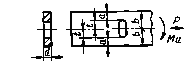
Конструктивные случаи для определения теоретическихкоэффициентов концентрации ασ и ατ пономограмме (приложение 3, черт. 48, 49)
| Вид выточки или надреза | Вид напряжения | Формула номинального напряжения | Ряд чисел для параметра
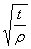 | Кривая для параметра
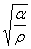 | Кривая для параметра
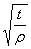 |
| 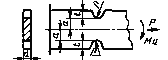
| Растяжение | 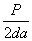
| b | 1 | - |
| Изгиб | 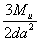
| b | 2 |
| 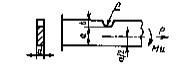
| Растяжение | 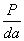
| b | 3 | |
| Изгиб | 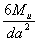
| b | 4 |
| 
| Растяжение | 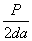
| b | 5 | - |
| Изгиб | 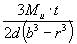
| a | 5 |
| 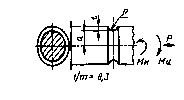
| Растяжение | 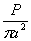
| b | 6 | - |
| Изгиб | 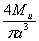
| b | 7 |
| Кручение | 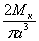
| a | 9 |
| 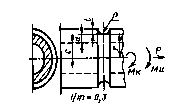
| Растяжение | 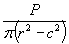
| b | 5 | 1 |
| Изгиб | 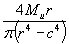
| b | 5 | 2 |
| Кручение | 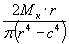
| a | 10 | 4 |
| 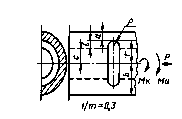
| Растяжение | 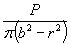
| b | 5 | 5 |
| Изгиб | 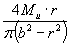
| b | 5 | 6 |
| Кручение | 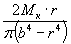
| a | 10 | 8 |
1.4.3. При обработкерезультатов на ЭВМ коэффициенты концентрации напряжений ασ для деталей, указанных на черт. 20-22, 27 и 28приложения 3, вычисляют по формуле
где коэффициенты A, B, С и Z определяютпо табл. 3 (а = d/2 или а= b/2),а в остальных случаях ασ определяют поформулам, приведенным на черт. 1-3, 6-11, 14-19 приложения 3.
Примечание. Формула (25) являетсяприближенной и дает отклонения до 10 %-20 % в запас прочности.
*Формулы 21-24. (Исключены, Изм. № 1).
Таблица 3
Значения коэффициентов для вычисления ασ по формуле (25)
| Коэффициенты | Форма образца (детали) | Двусторонний надрез (выточка) | Ступенчатый переход по галтели |
| изгиб | растяжение | кручение | изгиб | растяжение | кручение |
| А | Круглый | 0,20 | 0,22 | 0,7 | 0,62 | 0,62 | 3,4 |
| Плоский | - | 0,50 | 0,50 | - |
| В | Круглый | 2,75 | 1,37 | 10,3 | 5,80 | 3,50 | 19,0 |
| Плоский | 2,10 | 0,85 | - | 6,00 | 2,50 | - |
| С | Круглый | - | - | - | 0,20 | - | 1,0 |
| Z | 3,00 | 2,0 |
1.5.1. Относительный критерий подобия 0вычисляют по формуле
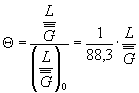 (26)
(26)
| где d0 = 7,5 мм; 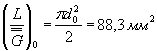 ; ; |
L выражается в мм,
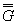 выражается в мм-1.
выражается в мм-1.
Значения функции 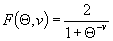 приведены в табл. 4или черт. 1приложения 4.
приведены в табл. 4или черт. 1приложения 4.
Таблица 4
Значения функции F (Θ, v)
| Θ | lgΘ | 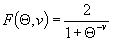 при v при v
|
| 0,04 | 0,08 | 0,10 | 0,12 | 0,16 | 0,20 |
| 0,0032 | -2,5 | 0,885 | 0,774 | 0,720 | 0,668 | 0,569 | 0,480 |
| 0,0100 | -2,0 | 0,908 | 0,813 | 0,774 | 0,730 | 0,647 | 0,569 |
| 0,0316 | -1,5 | 0,931 | 0,863 | 0,829 | 0,796 | 0,730 | 0,668 |
| 0,1000 | -1,0 | 0,954 | 0,908 | 0,836 | 0,836 | 0,818 | 0,774 |
| 0,3162 | -0,5 | 0,977 | 0,954 | 0,942 | 0,931 | 0,908 | 0,885 |
| 1,0000 | 0 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 3,1620 | 0,5 | 1,023 | 1,046 | 1,058 | 1,070 | 1,092 | 1,115 |
| 10,0000 | 1,0 | 1,046 | 1,092 | 1,115 | 1,137 | 1,182 | 1,226 |
| 31,6200 | 1,5 | 1,069 | 1,137 | 1,171 | 1,204 | 1,269 | 1,332 |
| 100,0000 | 2,0 | 1,092 | 1,182 | 1,226 | 1,269 | 1,353 | 1,430 |
| 316,2000 | 2,5 | 1,115 | 1,226 | 1,280 | 1,332 | 1,430 | 1,519 |
| 1000,0000 | 3,0 | 1,137 | 1,269 | 1,332 | 1,392 | 1,502 | 1,596 |
| 3162,0000 | 3,5 | 1,160 | 1,312 | 1,382 | 1,449 | 1,508 | 1,667 |
| 10000,0000 | 4,0 | 1,182 | 1,352 | 1,431 | 1,502 | 1,627 | 1,726 |
В формуле для определения F(Θ, v) параметр vпринимает значения vaσ при изгибе ирастяжении-сжатии и vτ - прикручении.
1.6.1. При круговом изгибе илирастяжении-сжатии, а также при кручении круглых стержней с кольцевымиканавками, с переходом от одного сечения к другому по галтели, с резьбой илигладких L =πd. При изгибе в одной плоскости круглых стержней L = 0,08 πd.
Если при растяжении-сжатии или изгибедеталей только часть периметра рабочего сечения прилегает к зоне повышеннойнапряженности, то L вычисляют поформулам, приведенным на черт. 2 приложения4.
Относительные градиенты напряжений 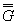 ,
,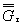 определяют по формулам, приведенным в табл. 1.
определяют по формулам, приведенным в табл. 1.
1.8.1. Значения vσ, vτ определяют по совокупности результатов испытаний наусталость образцов различных форм, размеров, уровней концентрации напряжений,изготовленных из металла одной плавки и испытанных при различных видахнагружения.
1.8.2. При отсутствии опытныхданных для конструкционных сталей величину vσ приближенновычисляют по формуле
vσ = 0,211 - 0,000143 σв при σв≤ 1300 МПа,
vσ = 0,025 при σв > 1300 МПа. (27)
При кручении дляконструкционных сталей величину vτ приближенно принимают равной
vτ = l,5 ∙ vσ. (28)
(Измененная редакция, Изм. № 1).
1.9.1. Значения коэффициента КFσ, характеризующего снижение пределов выносливости приухудшении качества обработки поверхности в зависимости от предела прочности и чистотыповерхности, для изгиба и растяжения-сжатия, определяют по черт. 3 приложения 4 или вычисляют по формуле
КFσ = 1 - 0,22 ∙ lg Rz(lg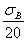 - 1) (σв в МПа). (29)
- 1) (σв в МПа). (29)
1.9.2. Значения коэффициента КFτ вычисляют по формуле
КFτ = 0,575 ∙ КFσ +0,425. (30)
1.10.1. Коэффициент Ккор, характеризующийснижение предела выносливости от влияния коррозии до испытания на усталость,приведен в зависимости от предела прочности на черт. 4 приложения 4.
На кривых указано количестводней, в течение которых образец подвергался воздействию коррозионной среды(пресной воды) до испытания на усталость.
1.10.2. Влияние коррозии приодновременном действии коррозионной среды и переменных напряжений представленов виде зависимости коэффициента Kкор отпредела прочности стали на черт. 5приложения 4.
1.10.3. Коэффициенты Kкор соответствуют определенной частоте испытания и числуциклов, указанных в подрисуночных подписях. При других частотах и базахиспытания следует вводить поправки в соответствии с экспериментальными данными.
1.11.1. Методика определениякоэффициента влияния поверхностного упрочнения Kv приведена в приложении 5.
1.11.2.Коэффициенты анизотропии, приведенные в табл. 5, учитывают, если первое главноенапряжение при изгибе и растяжении-сжатии направлено перпендикулярнонаправлению прокатки материала.
При кручении анизотропию неучитывают.
Таблица 5
Значения коэффициентов анизотропии KА
| σВ, МПа | ка | σВ, МПа | ка |
| До 600 | 0,90 | Св. 900 до 1200 | 0,83 |
| Св. 600 до 900 | 0,86 | » 1200 | 0,80 |
2.1. При наличии достаточного объема статистическойинформации для оценки коэффициента вариации пределов выносливости деталей машин(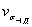 или
или 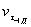 ), используя вычисленное для заданной базы по формуле (1) или (4) медианное значениепредела выносливости детали (
), используя вычисленное для заданной базы по формуле (1) или (4) медианное значениепредела выносливости детали (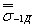 , или
, или 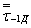 ), определяют пределы выносливостидетали на той же базе для любых заданных вероятностей разрушения Р в предположении справедливостинормального закона распределения по формулам:
), определяют пределы выносливостидетали на той же базе для любых заданных вероятностей разрушения Р в предположении справедливостинормального закона распределения по формулам:
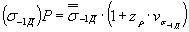 , (31)
, (31)
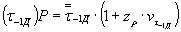 , (32)
, (32)
где zp - квантиль нормального распределения, соответствующаязаданной вероятности разрушения Р.
3.1. Коэффициент вариации пределавыносливости детали вычисляют по формуле
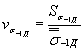 , (33)
, (33)
где 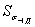 и
и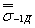 - среднее квадратическое отклонение и среднее (насовокупности всех плавок) значение предела выносливости детали соответственно.
- среднее квадратическое отклонение и среднее (насовокупности всех плавок) значение предела выносливости детали соответственно.
Результирующий коэффициент вариациипредела выносливости детали при отсутствии сварки, поверхностного упрочнения ипри стабильной технологии вычисляют по формуле
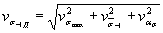 , (34)
, (34)
| где 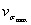 | - коэффициент вариации максимальных разрушающих напряжений в зоне концентрации, соответствующий пределам выносливости деталей (при испытании идентичных деталей, изготовленных из металла одной плавки, связанный со структурой неоднородностью металла (наличием различных фаз, включений, искажений кристаллической решетки и т.д.); |
| 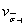
| - коэффициент вариации средних (в пределах одной плавки) значений пределов выносливости гладких лабораторных образцов диаметром 7,5 мм, учитывающий межплавочное рассеяние механических свойств металла и вычисляемый по формуле |
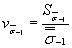 , (35)
, (35)
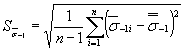 ; (36)
; (36)
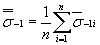 , (37)
, (37)
| где 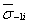 | - значение 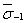 для i- плавки; для i- плавки; |
| n | - число плавок; |
| 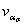
| - коэффициент вариации теоретического коэффициента концентрации напряжений ασ, учитывающий отклонения фактических размеров деталей (особенно в зонах концентрации напряжений) от номинальных (в пределах допусков). |
При нестабильной технологии,неоднородности свойств металла, наличии остаточных напряжений и технологическихдефектов коэффициенты вариации предела выносливости деталей 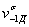 определяют путемпроведения усталостных испытаний деталей.
определяют путемпроведения усталостных испытаний деталей.
3.2.1. При достаточно стабильнойтехнологии, однородности свойств металла в объеме детали, отсутствии остаточныхнапряжений коэффициенты вариации максимальных разрушающих напряжений 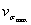 вычисляют по формуле
вычисляют по формуле
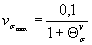 . (38)
. (38)
Коэффициент 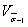 определяют постатистическим данным о межплавочном рассеянии пределов выносливости поформулам (35)-(37).
определяют постатистическим данным о межплавочном рассеянии пределов выносливости поформулам (35)-(37).
Если данных по межплавочному рассеяниювеличин 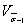 нет, то, учитываяпрактически линейную зависимость между пределами выносливости и пределамипрочности, в первом приближении допускают
нет, то, учитываяпрактически линейную зависимость между пределами выносливости и пределамипрочности, в первом приближении допускают
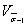 =
= 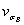
где 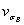 - коэффициентвариации предела прочности металла на множестве всех плавок (
- коэффициентвариации предела прочности металла на множестве всех плавок (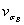 = 0,04-0,10).
= 0,04-0,10).
Колебания радиусов кривизны в зонеконцентрации напряжений ρхарактеризуются коэффициентами вариации vρ.Коэффициенты вариации находят по результатам измерения партии деталей (не менее30-50 шт.) в условиях производства.
Среднее значение 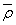 , среднее квадратическое отклонение sρ радиуса кривизны ρ и коэффициент вариации vρвычисляют по формулам:
, среднее квадратическое отклонение sρ радиуса кривизны ρ и коэффициент вариации vρвычисляют по формулам:
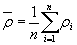 , (39)
, (39)
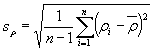 , (40)
, (40)
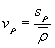 . (41)
. (41)
Зависимость ασ от ρпредставляют функцией
ασ = φ(ρ). (42)
Коэффициент вариации 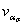 вычисляют по формуле
вычисляют по формуле
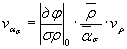 (43)
(43)
где 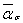 - среднее значение ασ, соответствующее ρ=
- среднее значение ασ, соответствующее ρ= 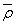 ;
;
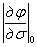 - абсолютное значение производной, котороесоответствует средним значениям определяющих параметров.
- абсолютное значение производной, котороесоответствует средним значениям определяющих параметров.
3.4.3. Для нахожденияпроизводной в выражении (43) допускается осуществлять линейную аппроксимациюфункции (42) в окрестности заданных значений параметров, используя уравнениепрямой, проходящей через две точки
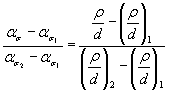 , (44)
, (44)
| где 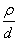 | - заданное значение отношения параметров ρ и d (вместо ρ/d может быть ρ/t и т.п.); |
| 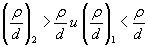
| - отношения 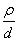 , близкие к заданному значению; , близкие к заданному значению; |
| 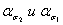
| - значения ασ, соответствующие (ρ/d)2и (ρ/d)1. |
4.1. Для расчета на прочностьлевую наклонную часть кривой усталости представляют в виде
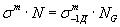 , (45)
, (45)
| где m | - показатель наклона кривой усталости в двойных логарифмических координатах; |
| NG | - абсцисса точки перелома кривой усталости. |
4.2. ВеличинаNG в большинстве случаев колеблетсяв пределах NG = 106 - 3 ∙ 106 циклов. Врасчетах на прочность при переменных напряжениях, когда отсутствуют данныенатурных усталостных испытаний, принимают в среднем NG =2∙ 106 циклов.
4.3. Величины m для деталей изменяются в пределах 3-20, при этом сростом коэффициента снижения предела выносливости K уменьшаетсяm. Зависимость между K и m принимают приближенно в виде
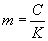 , (46)
, (46)
где
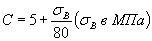 (47)
(47)
4.4. Значения Ψσ и Ψτ вычисляют по формулам:
Ψσ = 0,02 + 2 - 10-4 σB, (48)
Ψτ = 0,01 + 10-4 - σB, (49)
где σB в МПа.
Для деталей с концентрациейнапряжений коэффициенты влияния асимметрии цикла 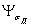 и
и 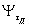 вычисляют поформулам:
вычисляют поформулам:
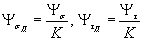 , (50)
, (50)
где K- коэффициент, определяемый по формулам (2), (5).
Для легированных сталейдопускается вычислять коэффициенты 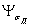 и
и 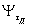 по формулам:
по формулам:
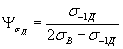 , (51)
, (51)
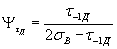 , (52)
, (52)
4.5. Предельные амплитуды длядеталей при асимметричном цикле нагружения вычисляют по формулам:
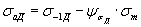 , (53)
, (53)
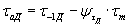 , (54)
, (54)
5.1. Расчет малоцикловой долговечностивыполняется на основе анализа местных деформаций. К малоцикловой относятобласть чисел циклов до разрушения < 5 ∙ 104-105,когда становится выраженным упругопластический характер деформированногосостояния конструкции. Рассматривают условия нагружения, при которыхмаксимальные деформации достигают 0,5 %-1,0 %.
5.2. При определениималоцикловой долговечности и оценке накопления повреждений должны бытьследующие данные:
- циклические упругопластические иодносторонне накопленные деформации в максимально напряженных зонахконструкции:
- располагаемая пластичность материала εf;
- кривая малоцикловой усталостиконструкционного материала (N =f(ε)(k)).
5.3.1. Напряженно-деформированноесостояние и его поцикловое изменение в максимально напряженных зонахконструкции определяют расчетным или экспериментальным методами, в том числе поданным тензометрических измерений на моделях и натурных конструкциях длязаданных или эквивалентных нагрузок.
5.3.2. Расчетное определениенапряженно-деформированного состояния элементов конструкций выполняетсярешением соответствующих задач малоциклового нагружения в циклической упруго-пластическойпостановке либо в замкнутой форме, либо численными методами.
5.3.3. Для приближенных оценокмалоцикловой прочности элементов конструкций, работающих при нагрузках,вызывающих в зонах концентрации напряжений выход материала за пределы упругости,деформации и напряжения приближенно определяют с использованиеминтерполяционных зависимостей типа
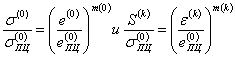 , (55)
, (55)
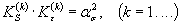 , (56)
, (56)
| где 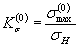 | - упругопластический коэффициент концентрации напряжений; |
| 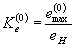
| - упругопластический коэффициент концентрации деформаций; |
| 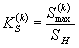
| - циклический упругопластический коэффициент концентрации напряжений; |
| 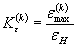
| - циклический упругопластический коэффициент концентрации деформаций. |
Зависимость используется для ασ ≤ 3,5. Прибольших значениях ασприменение формулы дает результаты, идущие в запас прочности.
Для вычисления значения циклическихупругопластических коэффициентов концентрации 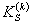 и
и 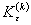 , кроме известных значений теоретического коэффициентаконцентрации ασ,необходимо знать зависимость напряжения от деформации при циклическомупругопластическом деформировании.
, кроме известных значений теоретического коэффициентаконцентрации ασ,необходимо знать зависимость напряжения от деформации при циклическомупругопластическом деформировании.
5.4.1. Диаграммастатического и циклического деформирования характеризует зависимость напряженияот деформации при статическом или циклическом нагружении. Диаграммыдеформирования определяют по данным испытаний при статическом или циклическомнагружении, проводимых по
ГОСТ 25.502
и
ГОСТ 1497
.
5.4.2. Аналитически диаграммыциклического деформирования интерпретируют в форме обобщенной диаграммыциклического деформирования. Обобщенная диаграмма циклического деформированияотражает зависимость напряжения от деформации по параметру числа полуцикловнагружения. Диаграмму рассматривают в координатах S- ε (черт. 1).Основное свойство обобщенной диаграммы заключается в том, что для мягкого,жесткого и промежуточных между мягким и жестким нагружениями все конечные итекущие точки диаграмм деформирования k-го полуцикла нагружения, полученные при различныхуровнях исходных деформаций, укладываются на одну и ту же для данного полуцикланагружения кривую. Схема обобщенной диаграммы деформирования приведена на черт.1.
Схема обобщенной диаграммы циклического деформирования
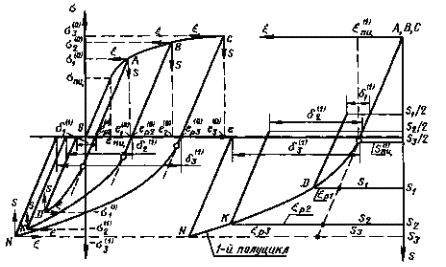
Черт. 1
Исходное нагружение происходит всоответствии с диаграммой статического деформирования О, A, B, С, рассматриваемой в координатах σ-е сначалом в точке О. Процессисходного нагружения доводят до определенного значения напряжений и деформаций,например до состояний А, В,С. Таким образом напряжения исходного нагружения составят 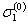 ,
, 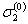 и
и 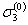 , а деформации -
, а деформации - 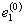 ,
, 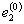 и
и 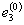 соответственно. Послеразгрузки, происходящей в соответствии с модулем упругости материала, остаютсявеличины пластических деформаций
соответственно. Послеразгрузки, происходящей в соответствии с модулем упругости материала, остаютсявеличины пластических деформаций 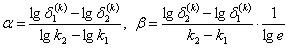 ,
, 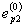 и
и 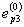 . Исходноенагружение и разгрузка образуют нулевой (k = 0) полуцикл нагружения.
. Исходноенагружение и разгрузка образуют нулевой (k = 0) полуцикл нагружения.
Реверс нагружения происходит по своей длякаждой степени исходного нагружения диаграмме деформирования, достигая,например, состояний D K, N, соответствующих напряжениям 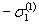 ,
, 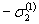 и
и 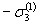 причем длясимметричного цикла мягкого нагружения
причем длясимметричного цикла мягкого нагружения 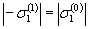 ,
,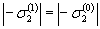 и
и 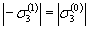 . Реверсивное нагружение и последующая разгрузка образуютпервый (k = 1) полуцикл нагружения, а совокупность нулевого ипервого полуциклов - первый (N = 1) цикл нагружения.
. Реверсивное нагружение и последующая разгрузка образуютпервый (k = 1) полуцикл нагружения, а совокупность нулевого ипервого полуциклов - первый (N = 1) цикл нагружения.
Обобщенная диаграмма циклического деформированиястроится для каждого отдельного полуцикла нагружения в координатах S- ε с началом в точке разгрузки и для каждогорассматриваемого состояния нагружения. Для первого (k = 1) полуцикла нагружения (при исходных уровняхнапряжений 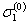 ,
, 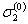 и
и 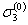 начало координат S- ε помещают в точки А, В, С. При этом кривая деформированиярассматриваемого полуцикла включает в себя участок нагружения этого полуцикла иучасток разгрузки предыдущего.
начало координат S- ε помещают в точки А, В, С. При этом кривая деформированиярассматриваемого полуцикла включает в себя участок нагружения этого полуцикла иучасток разгрузки предыдущего.
Для построения обобщенной диаграммыциклического деформирования точки начала разгрузки для данного полуцикланагружения совмещают. На правой части черт. 1 для k-1 точки А,В, С совмещены и образована единая зависимость междунапряжениями и деформациями A, B, C, D, K, N.
Аналогичные построения делают и дляпоследующих полуциклов нагружения. В общем случае, в связи с процессамициклического упрочнения или разупрочнения материала, обобщенные диаграммыдеформирования для различных полуциклов нагружения отличаются друг от друга.Обобщенная диаграмма циклического деформирования оказывается неизменной(начиная с k = 1) только для циклически стабильных материалов.
5.4.3. Для приближенныхрасчетов допускается использовать диаграммы циклического деформирования,образуемые удвоением статической диаграммы деформирования материала.
5.4.4. Аппроксимация диаграммдеформирования выполняется для расчетных приложений степенными функциями:
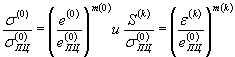 (57)
(57)
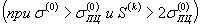 ,
,
| где 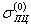 и и 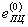 | - напряжение и деформация предела пропорциональности материала при статическом нагружении; |
| m(0) иm(k) | - показатели упрочнения материала в упругопластической области, определяемые по диаграммам статического и циклического деформирования при степенной аппроксимации. |
При этомциклический модуль упрочнения имеет вид:
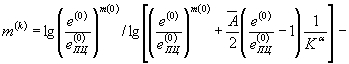 (58)
(58)
дляциклически упрочняющихся материалов, для которых m(k-1) < m(k)
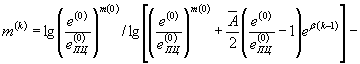 (59)
(59)
дляциклически разупрочняющихся материалов, для которых m(k-1) > m(k)
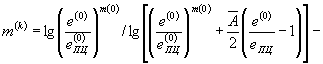 (60)
(60)
дляциклически стабилизирующихся материалов, у которых m(k-1) = m(k)
При линейной аппроксимации диаграммыстатического и циклического деформирования имеют вид:
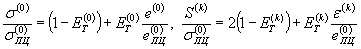 (61)
(61)
(при σ(0)> 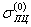 и S(k) >
и S(k) > 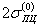 ),
),
| где 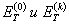 | - показатели упрочнения материала в упругопластической области, определяемые по диаграмме статического и циклического деформирования при линейной аппроксимации; |
| 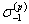
| - для циклически упрочняющихся материалов; |
| 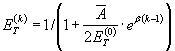
| - для циклически разупрочняющихся материалов; |
| 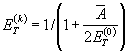
| - для циклически разупрочняющихся материалов. |
5.4.5. По статическим диаграммам деформирования определяют пределыпропорциональности, текучести и прочности, равномерное и общее удлинение (
ГОСТ 1497
), по диаграммам циклического деформирования - пределыпропорциональности и текучести по параметру числа циклов или полуцикловнагружения, коэффициенты 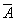 , α, β, характеризующие сопротивлениециклическому деформированию, циклическое упрочнение, разупрочнение,стабилизацию.
, α, β, характеризующие сопротивлениециклическому деформированию, циклическое упрочнение, разупрочнение,стабилизацию.
5.4.6. Коэффициент 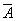 характеризует связь между деформациейисходного нагружения е(0) и шириной петли гистерезиса δ(1) впервом полуцикле при мягком нагружении. Определяют из выражения
характеризует связь между деформациейисходного нагружения е(0) и шириной петли гистерезиса δ(1) впервом полуцикле при мягком нагружении. Определяют из выражения
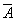 = δ(1)/ (е(0) -
= δ(1)/ (е(0) - 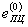 ). (62)
). (62)
Полученную совокупностьэкспериментальных величин 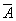 (по результатамиспытания серии порядка 5-10 образцов при различных значениях исходнойдеформации е(0))обрабатывают с использованием метода наименьших квадратов или другим способомосреднения.
(по результатамиспытания серии порядка 5-10 образцов при различных значениях исходнойдеформации е(0))обрабатывают с использованием метода наименьших квадратов или другим способомосреднения.
5.4.7. Коэффициенты α и β определяют по полученным при мягком нагруженииэкспериментальным данным lg δ(k) - lgk (для случая циклического упрочнения) иlg δ(k) - k (для циклического разупрочнения).Величины α или β для рассматриваемого образцавычисляют по формулам (черт. 2):
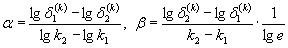 (63)
(63)
где δ(k) - ширина петли гистерезиса в k-м полуцикле нагружения.
Зависимость ширины петли гистерезиса от числаполуциклов нагружения
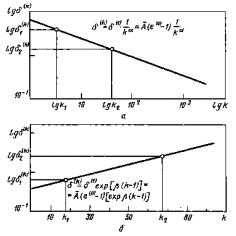
а -циклическое упрочнение; б - циклическоеразупрочнение
Черт. 2
Для расчетов в заданном диапазонемаксимальных деформаций рекомендуется применять средние коэффициенты α и β, полученные при различных значениях исходных деформаций взаданном диапазоне.
5.5.1. Располагаемуюпластичность материала (εf )определяют как
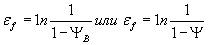 , (64)
, (64)
| где ΨB и Ψ | - коэффициенты уменьшения поперечного сечения, соответствующие достижению предела прочности или разрыву образца. Определяют по ГОСТ 1497. |
5.6.1. Кривуюмалоцикловой усталости определяют экспериментально по результатам испытанийсерии образцов при жестком нагружении по
ГОСТ 25.502
. Результаты представляют в виде зависимостидолговечности от циклической упругопластической или пластической деформации.
5.6.2. Аналитически кривуюмалоцикловой усталости выражают уравнениями:
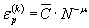 , (65)
, (65)
, (66)
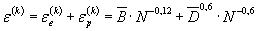 . (67)
. (67)
При этом зависимость долговечности отциклической пластической деформации (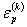 ) используют в диапазоне чисел циклов < 103 - 5∙ 103.
) используют в диапазоне чисел циклов < 103 - 5∙ 103.
Зависимость долговечности от циклическихупругопластических деформаций (ε(k) применяют во всем малоцикловом диапазоне чисел цикловнагружения (< 5 ∙ 104 - 105).
Коэффициенты в уравнениях определяют поэкспериментальным данным о долговечности при малоцикловом нагружении ссимметричным циклом деформаций.
5.6.3. Для приближенных расчетов кривоймалоцикловой усталости используют корреляционные зависимости, устанавливающиесвязь характеристик сопротивления малоцикловой усталости с прочностью ипластичностью материала при статическом разрыве образца. При этом принимаютследующие значения коэффициентов уравнений кривой малоцикловой усталости:
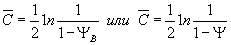 ;
;
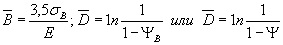 .
.
Показатель μ доя широкого круга конструкционныхсталей и сплавов, в первом приближении, равен 0,5-0,6.
Графики, соответствующие уравнениям (65)- (67) с учетом величин коэффициентов, приведены на черт. 3. Там же даны линии,характеризующие первое и второе слагаемые уравнений (66), (67).
Зависимость долговечности от величины пластической (а)
и упругопластической деформации (б,в) в цикле при ε(k) = const
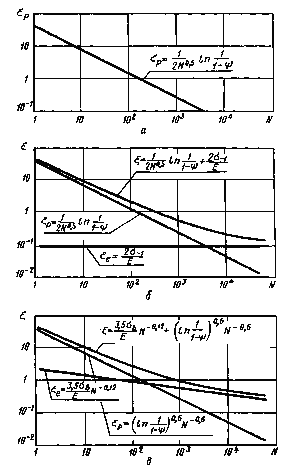
Черт. 3
5.6.4. Для получения расчетныхкривых используют, с целью обеспечения запасов прочности, минимальногарантированные по техническим условиям на материал величины Ψ, σB , σ-1. При наличии статистических данных в расчет вводят характеристики,соответствующие средним за вычетом трех стандартных отклонений.
5.6.5. В области числа цикловнагружения до разрушения 104 циклов асимметрию деформаций приопределении расчетных кривых малоцикловой усталости не учитывают, если еmах< 0,25εf.
При еmах > 0,25εf, вуравнениях кривых малоцикловой усталости используют коэффициенты, равные 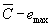 и
и 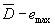 .
.
При числе циклов нагружения в диапазоне104-105 асимметрию цикла нагружения учитывают способом,аналогичным применяемому в многоцикловой области.
5.6.6. Масштабный эффект,влияние чистоты поверхности, коррозии и т.п. следует оценивать постановкойсоответствующих экспериментов.
ПРИЛОЖЕНИЕ1
Обязательное
ОБОЗНАЧЕНИЯ, ПРИМЕНЯЕМЫЕ В СТАНДАРТЕ
| σ-1 | - предел выносливости при симметричном цикле гладких лабораторных образцов диаметром d0 = 7,5 мм при изгибе с вращением, изготовленных по ГОСТ 25.502, МПа. |
| 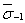
| - медианное значение σ-1 для образцов из металла одной плавки, МПа. |
| 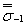
| - медианное значение предела выносливости на совокупности всех плавок металла данной марки гладких лабораторных образцов диаметром d0 = 7,5 мм, изготовленных из заготовок диаметром d, равным абсолютному размеру рассчитываемой детали, МПа. |
| К | - коэффициент снижения предела выносливости. |
| σ-1Д | - предел выносливости детали при симметричном цикле, выраженный в номинальных напряжениях, МПа. |
| 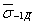
| - медианное значение σ-1Д, МПа. |
| 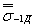
| - медианное значение предела выносливости детали на совокупности всех плавок металла данной марки, МПа. |
| (σ-1)Р | - значение σ-1 , соответствующее вероятности разрушения Р %, например (σ-1)10 при Р =10 %, МПа. |
| (σ-1Д)Р | - предел выносливости детали, соответствующий вероятности разрушения Р %, МПа. |
| 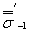
| - медианное значение предела выносливости гладких лабораторных образцов диаметром d0 = 7,5 мм, изготовленных из заготовок металла данной марки размерами 10-20 мм, МПа. |
| К1 | - коэффициент, учитывающий снижение механических свойств металла (σв, σт, σ-1) с ростом размеров заготовок. |
| σв | - временное сопротивление (предел прочности) стали данной марки при растяжении, МПа. |
| 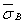
| - медианное значение предела прочности стали данной марки, определенное на образцах, изготовленных из заготовок диаметром d, равным абсолютному размеру рассчитываемой детали, МПа. |
| Kσ = σ-1d/σ-1д | - эффективный коэффициент концентрации напряжений. |
| Кdσ = σ-1d/ σ-1 | - коэффициент влияния абсолютных размеров поперечного сечения. |
| σ-1d | - предел выносливости образца без концентрации напряжений диаметром d, МПа. |
| 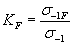
| - коэффициент влияния шероховатости поверхности, равный отношению предела выносливости образца с данным качеством поверхности σ-1f к пределу выносливости гладкого лабораторного образца. |
| 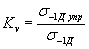
| - коэффициент влияния поверхностного упрочнения, равный отношению предела выносливости упрочненной детали σ-1Дупр к пределу выносливости неупрочненной детали σ -1д. |
| КА | - коэффициент анизотропии. |
| 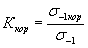
| - коэффициент влияния коррозии, равный отношению предела выносливости гладкого образца в условиях коррозии σ-1 кор к пределу выносливости образца при испытаниях в воздухе. |
| ξ', ξ" | - поправочные коэффициенты. |
| vσ | - постоянная для данного металла величина (при определенной температуре и частоте испытания), определяющая чувствительность к концентрации напряжений и влиянию абсолютных размеров поперечного сечения при изгибе или растяжении-сжатии. |
| L | - параметр рабочего сечения образца или детали или его часть, прилегающая к местам повышенной напряженности, мм. |
| 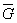
| - относительный градиент первого главного напряжения в зоне концентрации напряжений, мм-1. |
| 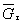
| - относительный градиент касательного напряжения, мм-1. |
| L/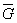 | - критерий подобия усталостного разрушения детали, мм2. |
| (L/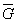 )0 )0 | - критерий подобия усталостного разрушения образца диаметром d0 = 7,5 мм, мм2. |
| 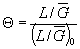
| - относительный критерий подобия усталостного разрушения. |
| ασ = σmax/σH | - теоретический коэффициент концентрации напряжений, равный отношению максимального напряжения в зоне концентрации σmax к номинальному напряжению σH, вычисленному по формулам сопротивления материалов (в предположении упругого распределения напряжений). |
| n = f(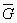 , σT) , σT) | - коэффициент, зависящий от значений относительного градиента напряжений и предела текучести. |
| σT | - предел текучести стали данной марки при растяжении, МПа. |
| q | - коэффициент чувствительности металла к концентрации напряжений. |
| 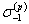
| - предел выносливости образцов при растяжении-сжатии, МПа. |
| А, В, С, Z | - постоянные коэффициенты. |
| 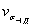
| - коэффициент вариации пределов выносливости деталей. |
| Zp | - квантиль нормального распределения, соответствующая заданной вероятности разрушения Р. |
| 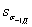
| - среднее квадратическое отклонение предела выносливости детали, МПа. |
| 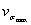
| - коэффициент вариации максимальных разрушающих напряжений в зоне концентрации. |
| 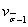
| - коэффициент вариации средних значений пределов выносливости образцов. |
| 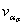
| - коэффициент вариации теоретического коэффициента концентрации напряжений ασ. |
| т | - показатель наклона левой ветви кривой усталости в двойных логарифмических координатах. |
| NG | - абсцисса точки перелома кривой усталости. |
| Ψσ | - коэффициент чувствительности к асимметрии цикла напряжений. |
| 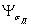
| - коэффициент чувствительности к асимметрии цикла напряжений для детали. |
| σад | - предельная амплитуда для детали при асимметричном цикле нагружения. |
| d0, d, dp, D, ρ , t, a, h, H | - размеры рабочего сечения образцов (деталей), мм. |
| εf | - располагаемая пластичность материала, %. |
| N | - число циклов нагружения. |
| k | - число полуциклов нагружения (k = 0, 1, 2, 3 ... ). |
| 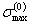
| - действительное максимальное напряжение в исходном нагружении (нулевой полуцикл), МПа. |
| σH | - номинальное напряжение, МПа. |
| 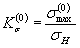
| - коэффициент концентрации напряжений в упругопластической области в исходном нагружении (нулевой полуцикл). |
| 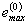
| - действительная максимальная упругопластическая деформация в исходном нагружении (нулевой полуцикл), %. |
| еH | - номинальная деформация в исходном нагружении (нулевой полуцикл), %. |
| 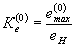
| - коэффициент концентрации деформаций в упругопластической области в исходном нагружении (нулевой полуцикл). |
| 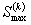
| - действительное максимальное напряжение в k-м полуцикле нагружения, МПа. |
| SH | - номинальное напряжение в k-м полуцикле нагружения, МПа. |
| 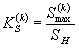
| - коэффициент концентрации напряжений в упругопластической области в k-м полуцикле нагружения. |
| 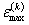
| - действительная максимальная упругопластическая деформация в k-м полуцикле нагружения, |
| εH | - номинальная деформация в k-м полуцикле нагружения, %. |
| 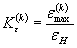
| - коэффициент концентрации деформаций в упругопластической области в k-м полуцикле нагружения. |
| e(0) | - уровень деформации в исходном нагружении гладких образцов, %. |
| σ(0) | - уровень напряжений в исходном нагружении гладких образцов, МПа. |
| 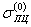
| - предел пропорциональности в исходном нагружении, определенный при допуске на пластическую деформацию 0,02 % в координатах σ - е, МПа. |
| 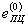
| - деформация, соответствующая пределу пропорциональности в исходном нагружении в координатах σ - е, %. |
| 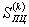
| - предел пропорциональности в k-м полуцикле нагружения в координатах S - ε, МПа. |
| 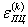
| - деформация, соответствующая пределу пропорциональности в k-м полуцикле нагружения в координатах S - ε, %. |
| 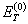
| - показатель упрочнения в упругопластической области при линейной аппроксимации диаграммы статического деформирования. |
| 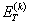
| - показатель упрочнения в упругопластической области при линейной аппроксимации диаграммы циклического деформирования в k-м полуцикле нагружения. |
| т(0) | - показатель упрочнения в упругопластической области при степенной аппроксимации диаграммы статического деформирования. |
| m(k) | - показатель упрочнения в упругопластической области при степенной аппроксимации диаграммы циклического деформирования в k-м полуцикле нагружения. |
| δ(1) | - ширина петли гистерезиса в 1-м полуцикле нагружения, %. |
| δ(k) | - ширина петли гистерезиса в k-м полуцикле нагружения, %. |
| e(k) | - упругопластическая деформация, накопленная после k-го полуцикла нагружения, %. |
| 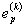
| - пластическая деформация, накопленная после k-го полуцикла нагружения, %. |
| 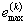
| - максимальная упругопластическая деформация, накопленная за k полуциклов нагружения, |
| 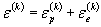
| - размах упругопластической деформации в k-м полуцикле нагружения, %. |
| 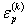
| - размах пластической деформации в k-м полуцикле нагружения, равный σ(k). |
| 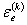
| - упругая деформация в k-м полуцикле нагружения, %, равная S(k)/Е. |
| Ψ | - относительное сужение площади поперечного сечения образца при статическом растяжении, %. |
| ΨB | - относительное сужение площади поперечного сечения образца, соответствующее σв, %. |
| Е | - модуль упругости материала, МПа. |
| 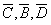
| - коэффициенты уравнений кривой малоцикловой усталости. |
Примечание. При кручении обозначенияаналогичны с заменой σ на τ, например τ-1?τ-1ди т.д.
ПРИЛОЖЕНИЕ 2
Обязательное
ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНЫХ КОЭФФИЦИЕНТОВ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ КσКτ ОТНОШЕНИЙ 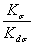 ,
, 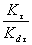 , КОЭФФИЦИЕНТОВ n, q, К1,И К3
, КОЭФФИЦИЕНТОВ n, q, К1,И К3
Валы с напрессованными деталями при изгибе
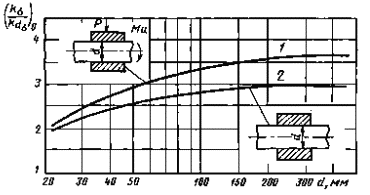
σв = 500 МПа; Р ≥ 30 МПа; 1 - черезнапрессованную деталь передается сила или момент; 2 - через напрессованную деталь не передается усилий
Черт. 1
Поправочный коэффициент 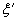 на предел прочности σB (к черт. 1)
на предел прочности σB (к черт. 1)
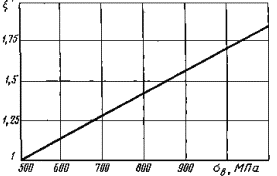
Черт. 2
Поправочный коэффициент 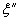 на давлениенапрессовки Р (к черт. 1)
на давлениенапрессовки Р (к черт. 1)
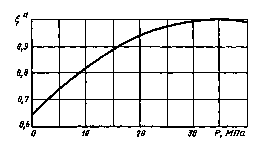
Черт. 3
Валы с поперечным отверстием при изгибе
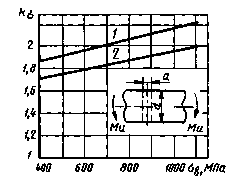
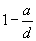 = 0,05-0,10; 2 -
= 0,05-0,10; 2 - 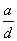 = 0,15-0,25;
= 0,15-0,25;
при d= 30-50 мм
Черт. 4
Валы с поперечным отверстием при кручении
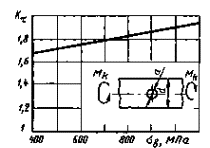
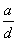 = 0,05 - 0,25;
= 0,05 - 0,25;
при d = 30-50 мм
Черт. 5
Валы с поперечным отверстием при растяжении-сжатии
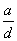 = 0,20-0,45; d = 15 мм;
= 0,20-0,45; d = 15 мм; 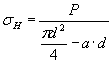
Черт. 6
Валы с V-образной кольцевойвыточкой
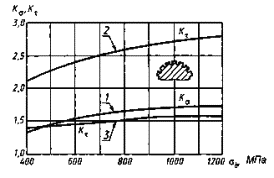
1 -прямобочные и эвольвентные шлицы;
2 - прямобочные шлицы; 3 - эвольвентные шлицы
Черт. 7
КоэффициентыКσ, Кτдля валовсо шпоночными пазами типов А и В
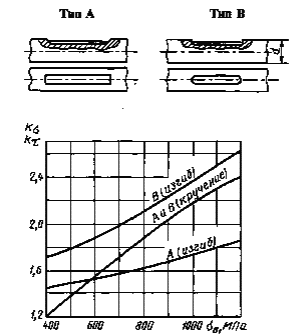
Черт. 13*
* Черт.8-12. (Исключены, Изм. № 1)
Коэффициенты n
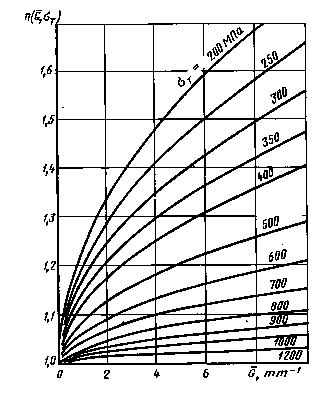
Черт. 14
Коэффициенты q
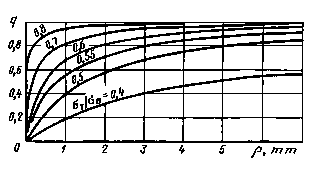
Черт. 15
Коэффициенты К1
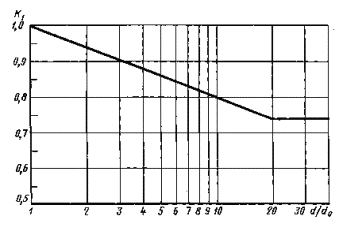
Черт. 16
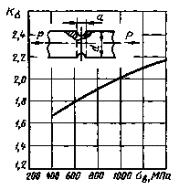
Пластины с двухсторонним надрезом при растяжении(черт. 1-3)
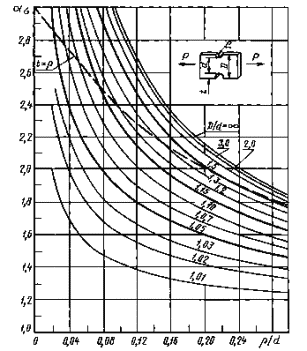
Пунктирнаялиния t = ρ -полуокружность;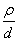 = 0,02-0,30
= 0,02-0,30
Черт. 1
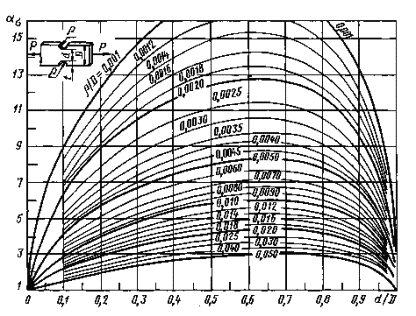
0,001 ≤ ρ/D ≤ 0,050
Черт. 2
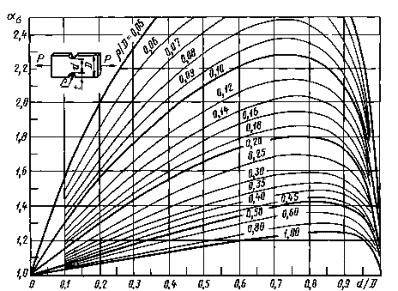
0,05 ≤ρ/D ≤ 1,00
Черт. 3
Формулы к черт. 1-3
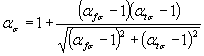
где 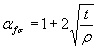 ;
;
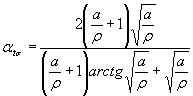
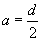
Пластины типов а и в при растяжении
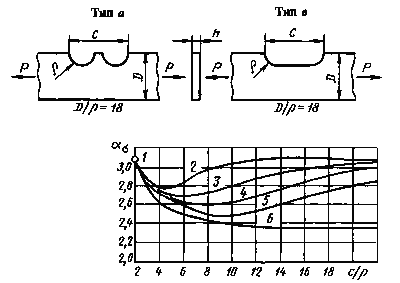
1-5- пластины типа а (1 - однократный надрез; 2 - двухкратный надрез; 3 - трехкратный надрез; 4 - четырехкратный надрез; 5 - пятикратный надрез); 6 - пластины типа в
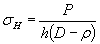
Черт. 4
Коэффициент разгрузки γ
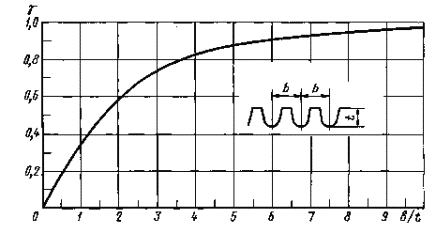
Черт. 5
Примечание. Коэффициент у для многократногонадреза находят по диаграммам для однократного надреза при глубине t' = γ ∙ t, где t - глубина многократного надреза, t'- глубина эквивалентного однократного надреза.
Валы с выточкой при растяжении (черт. 6-8)
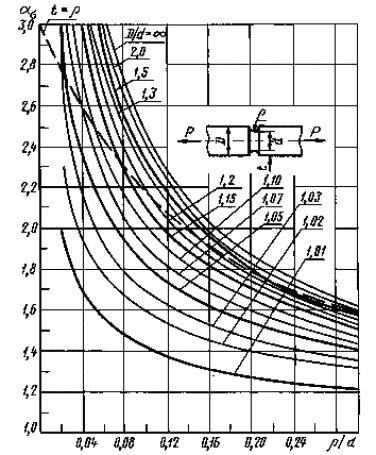
ρ/d = 0,02 - 0,30
Черт. 6
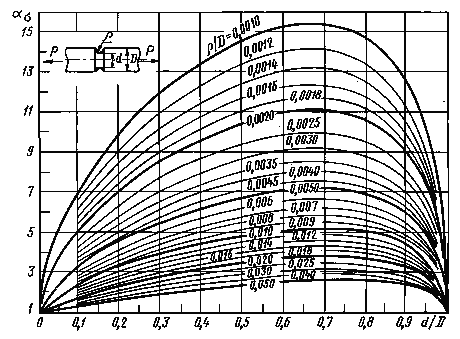
0,001 < ρ/D< 0,050
Черт. 7
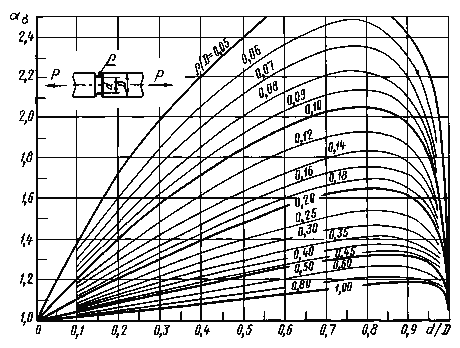
0,050 ≤ ρ/D ≤ 1,00
Черт. 8
Формулы к черт. 6-8
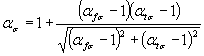
где 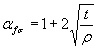 ,
,
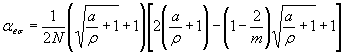 ,
,
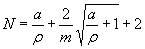 ,
,
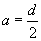 ,
, 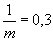 .
.
Пластины с двусторонним надрезом при изгибе (черт. 9-11)
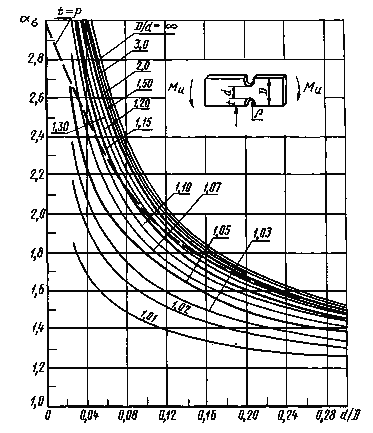
ρ/d = 0,02-0,30
Черт. 9
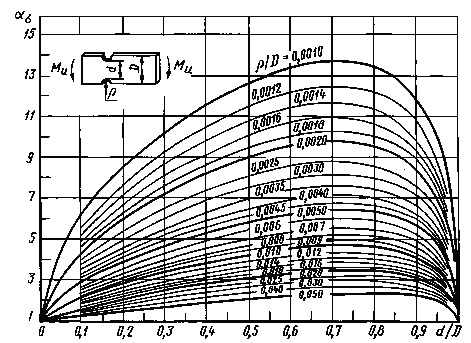
0,001≤ ρ/D ≤0,050
Черт.10
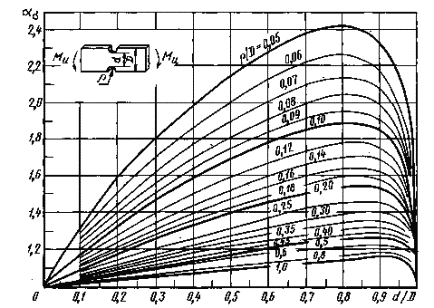
0,050≤ ρ/D ≤ 1,00
Черт. 11
Формулы кчерт. 9-11
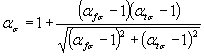
где 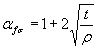 ,
,
Влияние угланадреза на коэффициент концентрации напряжений при изгибе пластины содносторонним надрезом
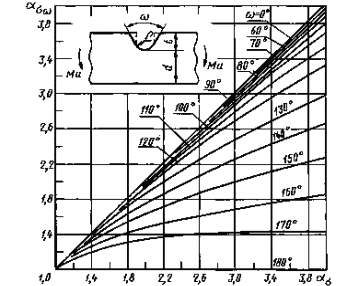
ασ - коэффициентконцентрации напряжений для надреза с углом ω= 0 (пунктир на схеме пластины); 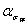 - коэфффициентконцентрации напряжений для надреза с углом ωпри тех же размерах
- коэфффициентконцентрации напряжений для надреза с углом ωпри тех же размерах
Черт.12
Тонкий листс двухсторонним надрезом при изгибе в плоскости, перпендикулярной плоскостилиста (t/hзначительно)
Черт.13
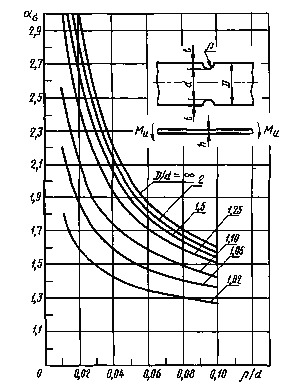
Валы свыточкой при изгибе (черт. 14-16)
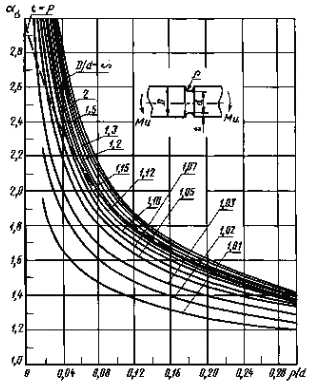
ρ/d =0,02-0,30
Черт. 14
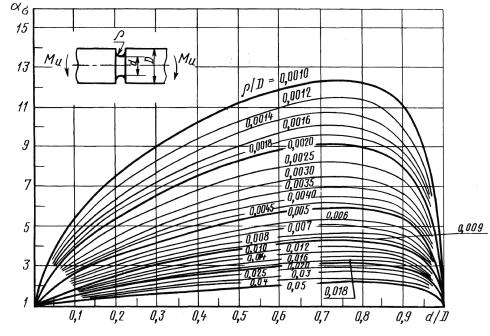
0,001 ≤ ρ/D ≤ 0,050
Черт.15
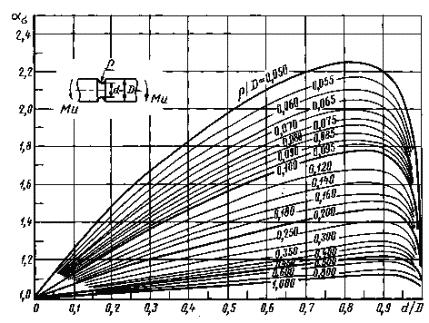
0,050 ≤ ρ/D ≤1,00
Черт. 16
Формулы кчерт. 14-16
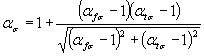
где 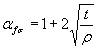 ,
,
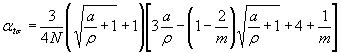 ,
,
| 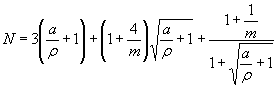 . .
|
Валы свыточкой при кручении (черт. 17-19)
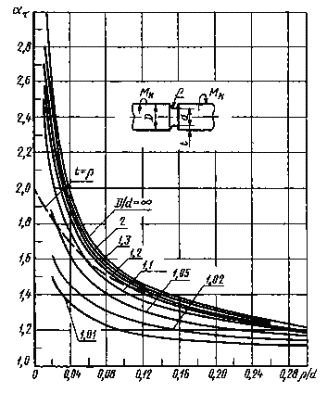
ρ/d = 0,02 -0,30
Черт. 17
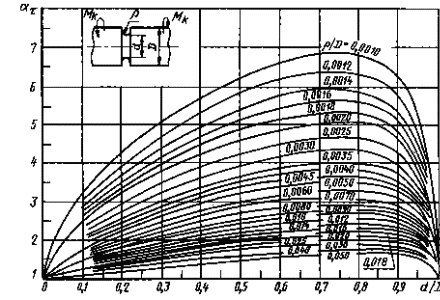
0,001 ≤ ρ/D ≤ 0,050
Черт. 18
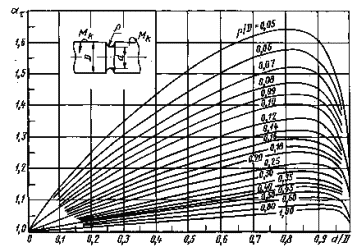
0,05 ≤ ρ/D ≤1,00
Черт. 19
Формулы кчерт. 17-19
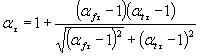
где 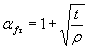 ,
,
| 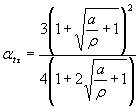 . .
|
Симметричнаяступенчатая пластина с галтелями при растяжении
(по данным поляризационно-оптических измерений)
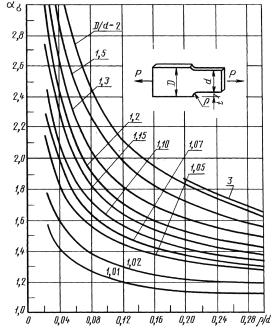
Черт. 20
Ступенчатыйвал с галтелью при растяжении (сжатии)
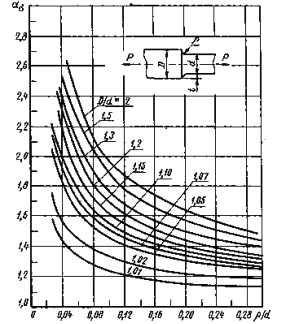
Черт.21
Ступенчатаяпластина с галтелями при изгибе (по данным поляризационно-оптических измерений)
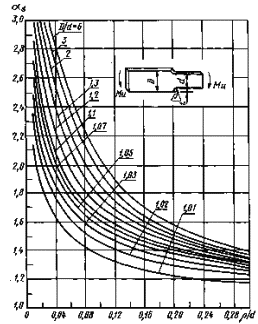
Черт. 22
Влияниедлины выступа пластины на коэффициент концентрации напряжений для ступенчатойпластины с галтелями при изгибе (черт. 23-25)
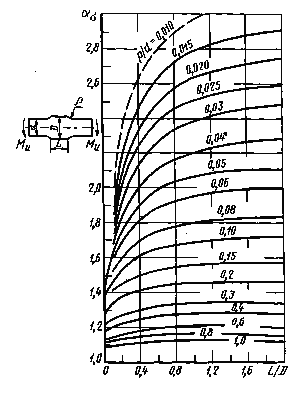
D/d = 1,25
Черт. 23
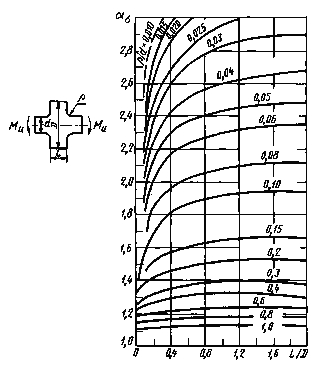
D/d = 2
Черт. 24
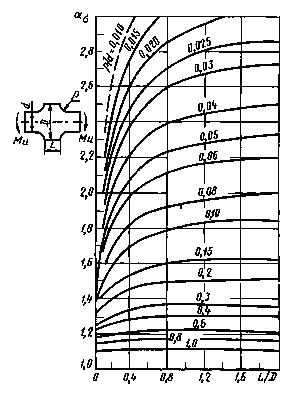
D/d = 3
Черт. 25
Ступенчатаяпластина с эллиптической галтелью при изгибе
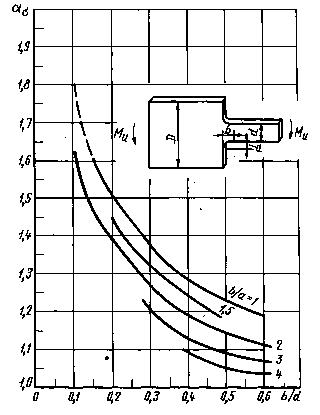
D/d = 3 (по даннымполяризационно-оптических измерений)
Черт. 26
Ступенчатыйвал с галтелью при изгибе
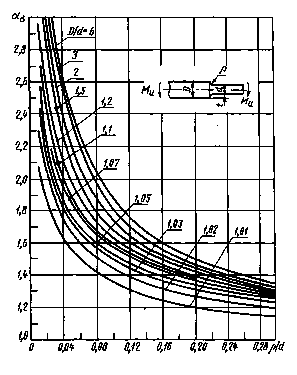
Черт. 27
Ступенчатыйвал с галтелью при кручении (измерения по методу электрических аналогий)
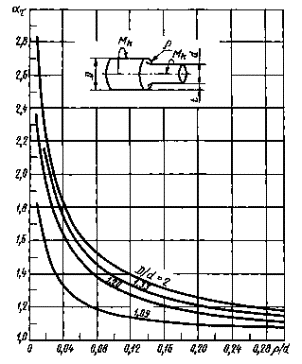
Черт. 28
Тонкаяпластина ограниченной ширины с поперечным отверстием при растяжении (теоретическоерешение)
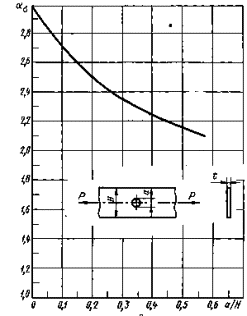
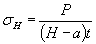
Черт. 29
Тонкаяпластина неограниченной ширины с поперечным отверстием при изгибе (теоретическоерешение)
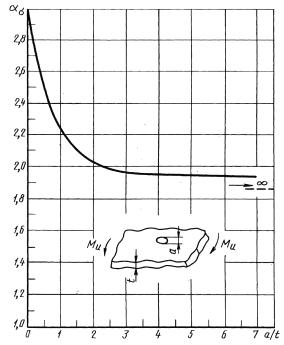
Черт. 30
Тонкаяпластина ограниченной ширины с поперечным отверстием при изгибе
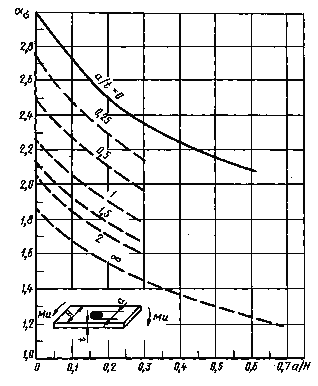
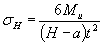
Черт.31
Вал споперечным отверстием при изгибе (измерения с помощью тензометров)
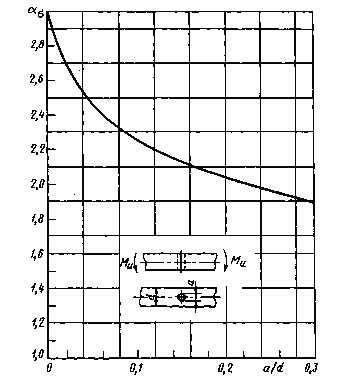
Черт.32
Пластины сТ-образной головкой
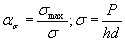 (черт. 33-37)
(черт. 33-37)
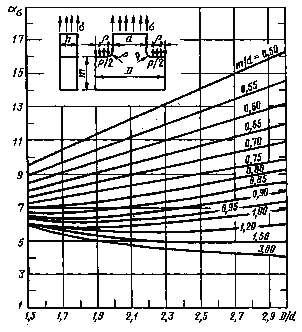
ρ/d =0,050(измерения с помощью поляризационно-оптического метода)
Черт.33
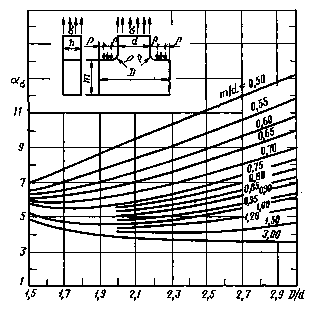
ρ/d = 0,075
Черт.34
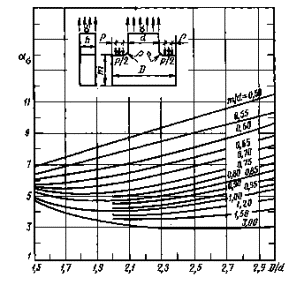
ρ/d =0,1
Черт. 35
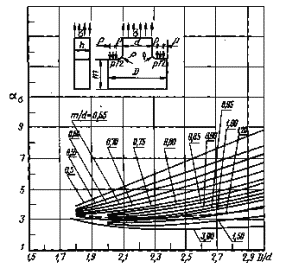
ρ/d =0,2
Черт. 36
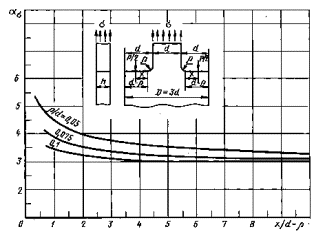
Примечание. Координата точки приложениясосредоточенной силы Р/2 пооси X-переменная
Черт. 37
Пластина споперечной прорезью при изгибе
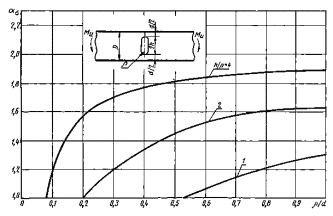
Черт. 38
Пластина споперечной прорезью при растяжении
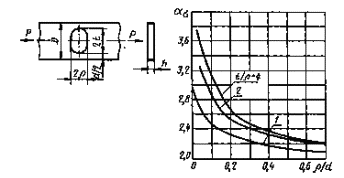
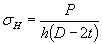 .
.
 .
.
Черт. 39
Пластина содносторонним надрезом при изгибе
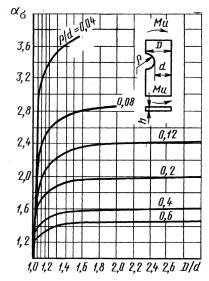
| 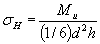 . .
|
Черт. 40
Пластина сэксцентрично расположенным отверстием толщиной h при растяжении
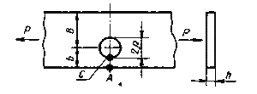
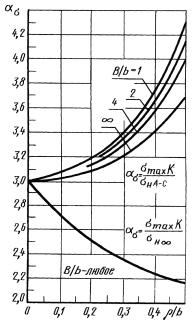
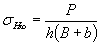 .
.
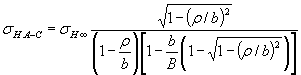
Черт.41
Вал споперечным отверстием при растяжении(1) и изгибе (2)
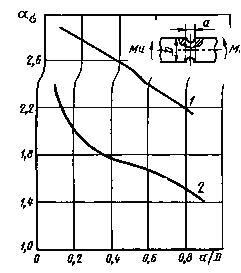
Черт.42
Вал с пазомдля призматической шпонки при кручении
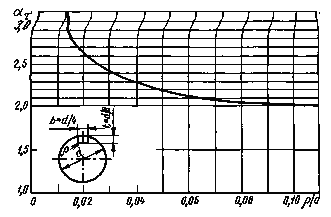
Черт. 43
Кольцо снаружной единичной нагрузкой Р
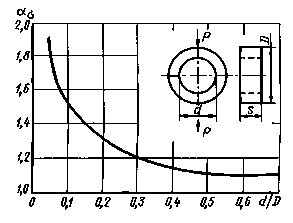
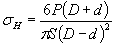 .
.
Черт.44
Уголок сравными по толщине полками при изгибающем моменте Р ∙ е
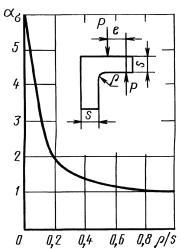
Черт.45
Уголок снеравными по толщине полками при изгибе от единичной нагрузки Р
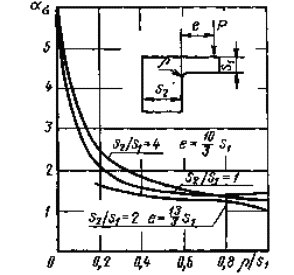
Черт.46
Уголок сприблизительно равными по толщине полками при изгибе от единичной нагрузки Р
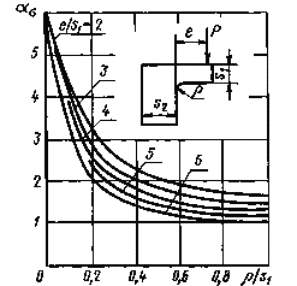
Черт. 47
Номограммадля определения теоретического коэффициента концентрации
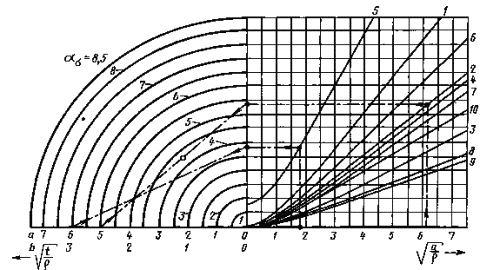
Черт. 48
Номограммадля кольцевых выточек с осевым отверстием
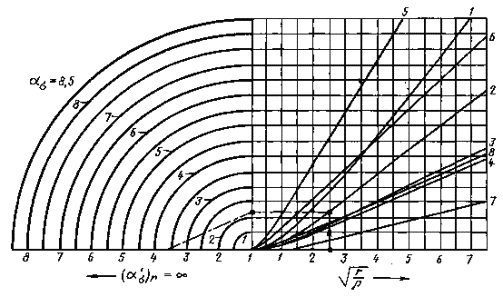
Черт. 49
ПРИЛОЖЕНИЯ 1-3. (Измененная редакция, Изм. № 1).
Значенияфункции F (Θ , v)
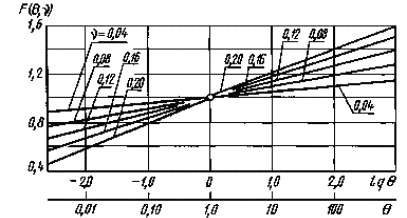
Черт. 1
Схемы к определению параметра L
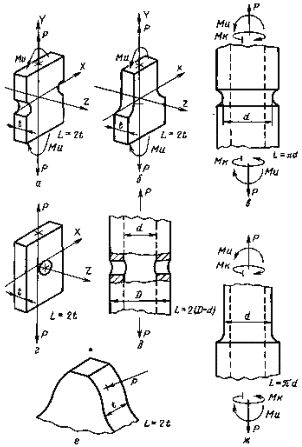
Черт. 2
Значения коэффициентов KF
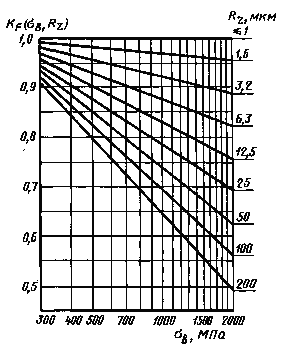
Черт. 3
Примечание. При наличии окалины используютнижнюю прямую (Rz = 200 мкм).
Влияние коррозии доиспытания на усталость на предел выносливости стальных образцов (при изгибе с вращениемна базе 107 циклов при частоте нагружения 30-50 Гц)
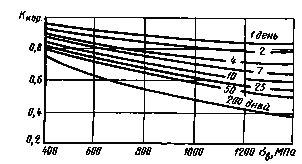
Черт. 4
Влияние коррозии в процессеиспытания на предел выносливости стальных образцов при изгибе с вращением(осредненные кривые) на базе 107 циклов при частоте нагружения 30-50Гц
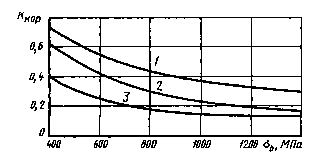
1 - пресная вода (наличие концентрации напряжений); 2 -пресная вода (отсутствие концентрации напряжений); 3 - морская вода (отсутствиеконцентрации напряжений)
Черт. 5
ПРИЛОЖЕНИЕ5
Рекомендуемое
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ВЛИЯНИЯ ПОВЕРХНОСТНОГО УПРОЧНЕНИЯ Kv
1. Коэффициентывлияния поверхностного упрочнения на предел выносливости вычисляют по формуле
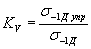 , (1)
, (1)
| где σ-1Дупр | - предел выносливости упрочненных деталей; |
| σ-1Д | - предел выносливости неупрочненных деталей. |
Средние значения KV для различных методов поверхностногоупрочнения образцов из углеродистых и легированных конструкционных сталейприведены в табл. 1-3.
Таблица 1
Влияние поверхностной закалки токами высокой частоты
(изгиб с вращением, глубина закаленного слоя 0,9-1,5мм)
| Вид образца | КV для образца диаметром |
| 7-20 мм | 30-40 мм |
| Без концентрации напряжений | 1,3-1,6 | 1,2-1,5 |
| С концентрацией напряжений | 1,6-2,8 | 1,5-2,5 |
Таблица 2
Влияние химико-термической обработки
| Характеристика химико-термической обработки | Вид образца | КV для образцов диаметром |
| 8-15 мм | 10 мм | 30-40 мм |
| Азотирование при глубине слоя 0,1-0,4 мм твердости слоя 730.. .970 НВ | Без концентрации напряжений | 1,15-1,25 | - | 1,10-1,15 |
| С концентрацией напряжений (поперечное, отверстие, надрез) | 1,90-3,00 | 1,30-2,00 |
| Цементация при глубине слоя 0,2-0,6 мм | Без концентрации напряжений | 1,20-2,10 | 1,10-1,50 |
| С концентрацией напряжений | 1,50-2,50 | 1,20-2,00 |
| Цианирование при глубине слоя 0,2 мм | Без концентрации напряжений | - | 1,80 | - |
Таблица 3
Влияние поверхностного наклепа
| Способ обработки | Вид образца | КV для образца диаметром |
| 7-20 мм | 30-40 мм |
| Обкатка роликом | Без концентрации напряжений | 1,20-1,40 | 1,10-1,25 |
| С концентрацией напряжений | 1,50-2,20 | 1,30-1,80 |
| Обдувка дробью | Без концентрации напряжений | 1,10-1,30 | 1,10-1,20 |
| С концентрацией напряжений | 1,40-2,50 | 1,10-1,50 |
2. Приведенные в п. 1значения КV соответствуют оптимальной технологии упрочнения иотсутствию технологических дефектов. При неправильной технологии упрочнения илиналичии дефектов (обрыв поверхностного закаленного слоя в зоне концентрациинапряжений, обезуглероживание поверхностного слоя, шлифовочные прижоги и другиедефекты) может получиться не повышение, а даже снижение пределов выносливости.
Поэтому введение в формулу (2) (см. п. 1.1)коэффициентов KV возможно только при проведении исследований для обоснованиятехнологических режимов упрочнения применительно к конкретной детали и приполучении стабильного эффекта упрочнения (в смысле повышения пределавыносливости) в условиях производства.
Пример1.
Определить среднее значение и коэффициентвариации предела выносливости вала при изгибе с вращением в месте переходаодного сечения к другому по галтели, показанного на черт. 1.
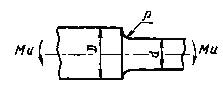
D = 120мм; d = 100мм; ρ = (10 ± 2) мм
Черт 1
Вал изготовлен из стали 45, σв = 650 МПа.
Дано: 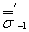 = 300 МПа;
= 300 МПа;  = 0,07; поверхностному упрочнению вал неподвергается. Вал изготовлен тонкой обточкой (Rz
= 0,07; поверхностному упрочнению вал неподвергается. Вал изготовлен тонкой обточкой (Rz 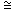 6,3 мкм).
6,3 мкм).
Находим значение ασ по черт. 27 приложения 3.
Для 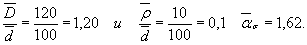
2. Определяем значение 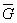 по формуле табл. 1 настоящего стандарта
по формуле табл. 1 настоящего стандарта
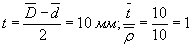 ;
;
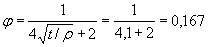 ;
;
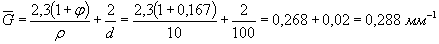 .
.
3. Вычисляем значение Θ.
L = πd=314 мм - при изгибе с вращением круглого вала;
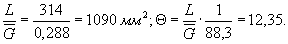
4. Для стали 45 можно принять vσ = 0,211-0,000143∙ 650 = 0,12. По табл. 4 или по черт. 1 (приложение 4) находим при Θ = 12,35; F(Θ , vσ) = 1,15.
5. Определяем Kσ/Kdσпо формуле (11) настоящего стандарта
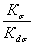 = ασ ∙F(Θ, vσ) = 1,62 - 1,15 =1,86.
= ασ ∙F(Θ, vσ) = 1,62 - 1,15 =1,86.
4, 5. (Измененная редакция, Изм. № 1).
6. Для случая тонкой обточки (Rz = 6,3 мкм) по черт. 3 (приложения 4) для σв = 650 МПа находим: KF =0,91.
7. Определяем значение К по формуле (2)настоящего стандарта
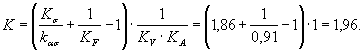
(Измененнаяредакция, Изм. № 1).
8. Коэффициент анизотропии КА= 1, KV= 1.
9. Коэффициент К1 = 1.
(Измененнаяредакция, Изм. № 1).
10.(Исключен,Изм. № 1).
11. Среднее значение пределавыносливости вала составит:
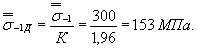
Коэффициент вариации 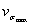 находим по формуле (38) настоящего стандарта
находим по формуле (38) настоящего стандарта
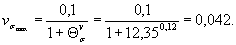
Для подсчета коэффициента вариации 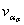 находим по черт. 27 (приложения 3) значения ασ при D/d = 1,2 и двух значениях, близких к 0,1, например при
находим по черт. 27 (приложения 3) значения ασ при D/d = 1,2 и двух значениях, близких к 0,1, например при
(ρ/d)1 = 0,09, 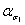 = l,67,(ρ/d)2 =0,11,
= l,67,(ρ/d)2 =0,11, 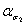 = 1,59.
= 1,59.
По формуле (44) настоящего стандарта находим
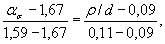
откуда ασ = 2,03-4 ∙ ρ/d.
По формуле (43) настоящего стандарта получаем
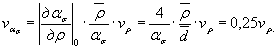
Принимая отклонения радиуса ± 2мм за 3Sρ,получим:
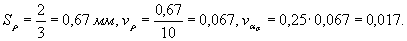
Из-за отсутствия данных коэффициентвариации 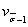 принимаем равным
принимаем равным
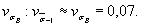
Общий коэффициент вариации предела выносливостивала составит
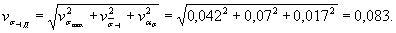
(Измененнаяредакция, Изм. № 1).
Пример2.
Определить среднее значение пределавыносливости пластины с отверстием при растяжении-сжатии, показанной на черт.2.
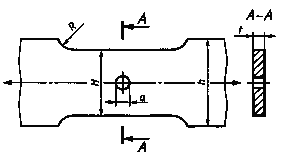
Н = 100мм; α = 10+0,1мм; t = 12мм.
Черт. 2
Пластина изготовлена из стали марки Ст.3.Rz = 50 мкм.
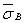 = 402 МПа;
= 402 МПа; 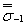 = 185 МПа;
= 185 МПа; 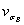 = 0,06;
= 0,06; 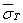 = 270 МПа.
= 270 МПа.
(Измененнаяредакция, Изм. № 1).
1. Определяем значение ασ на черт. 29 (приложения 3)
Для 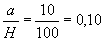 ; ασ=2,73.
; ασ=2,73.
2. Определяем значение 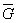 по формуле табл. 1 настоящего стандарта
по формуле табл. 1 настоящего стандарта
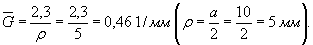 .
.
3. Находим коэффициент nпо черт. 14 (приложения 2)
n = 1,12.
4. Определяем коэффициент Кσ по формуле (13)настоящего стандарта
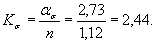
5. Определяем параметр vσ по формуле (27) настоящего стандарта vσ = 0,211 -0,000143 ∙ 402 = 0,15.
(Измененная редакция, Изм. № 1).
5а. Определяем значения L, 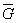 и ΘГЛ для аналогичной пластины без концентратора напряженийпо табл. 1 и приложению 4 (черт. 2) настоящего стандарта
и ΘГЛ для аналогичной пластины без концентратора напряженийпо табл. 1 и приложению 4 (черт. 2) настоящего стандарта
L = 2t = 2 ∙ 12 = 24мм,
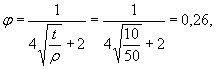
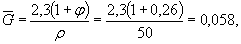
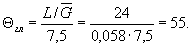
(Введен дополнительно, Изм. № 1).
6. Определяем коэффициент Кdσ по формуле (12)настоящего стандарта
Kdσ = 0,5(1 +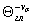 ) = 0,5(1 + 55-0,15) = 0,77,
) = 0,5(1 + 55-0,15) = 0,77,
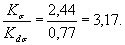
(Измененнаяредакция, Изм. № 1).
По черт. 3 (приложение 4) находим KF=0,89.
Коэффициент Kопределяем по формуле (2) настоящего стандарта
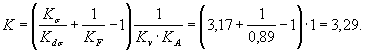
(Измененнаяредакция, Изм. № 1).
9. 10. (Исключены, Изм. № 1).
11. Средний предел выносливости пластиныс отверстием вычисляем по формуле (1) настоящего стандарта (коэффициент К1 = 1 для углеродистых сталей)
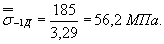
(Измененнаяредакция, Изм. № 1).
Пример3.
Определить среднее значение пределавыносливости вала с канавкой при кручении (черт. 3).
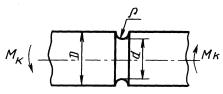
D =200 мм; d = 180 мм; ρ= (1,8 ± 0,3) мм.
Черт. 3
Вал изготовлен из стали марки 40ХН. σв = 820 МПа, σт = 650 МПа, 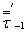 = 240 МПа,
= 240 МПа, 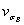 = 0,07; канавкуизготовляют тонкой обточкой и поверхностному упрочнению не подвергают (Rz = 6,3 мкм).
= 0,07; канавкуизготовляют тонкой обточкой и поверхностному упрочнению не подвергают (Rz = 6,3 мкм).
1. Находим значение ατ по черт. 18 (приложения 3) при
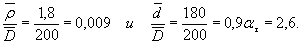
2. Определяем значение q по черт. 15 (приложения 2)
q = 0,96.
3. Величину Кτ определяем по формуле (19) настоящего стандарта
Кτ = 1 + q(ατ - 1) = 1+ 0,96(2,6-1) = 2,54.
4. Для d = 180 ммпринимаем К2 = 0,8.
5. Определяем параметры vσ и vτ по формулам (27) и (28) настоящего стандарта:
vσ = 0,211 - 0,000143 ∙ 820 = 0,09,
vτ = 1,5 - 0,09 = 0,140.
(Измененнаяредакция, Изм. № 1).
5.1. Определяем значение Θглпо п.1.2.3.1 настоящего стандарта
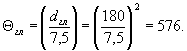
5.2. Вычисляем коэффициент Кdτ по формуле (12) настоящего стандарта
Кdτ = 0,5(1 + 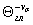 ) = 0,5(1 + 576-0,14) = 0,71.
) = 0,5(1 + 576-0,14) = 0,71.
5.3. Определяем отношение 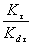
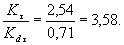
5.1-5.3. (Введены дополнительно, Изм. № 1).
6. Из черт. 3 (приложения 4) определяемкоэффициент KF для тонкойобточки (Rz = 6,3 мкм)
KF=0,89.
7. При отсутствии поверхностногоупрочнения
KV =1
8. При кручении КА = 1 (см. п.1.11.2).
9. Коэффициент К равен
К = (3,58+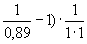 =3,7.
=3,7.
(Измененнаяредакция, Изм. № 1).
10. Принимаем коэффициент К1 для d = 180 ммравным 0,74 (п.1.3.1).
11. Вычисляем предел выносливостиматериала заготовки по формуле (6)настоящего стандарта
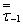 = 0,74 ∙ 240 = 178 МПа.
= 0,74 ∙ 240 = 178 МПа.
12. Вычисляем средний предел выносливостивала по формуле (4)настоящего стандарта
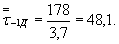
(Измененнаяредакция, Изм. № 1).
Настоящий стандарт являетсяунифицированным стандартом СССР и ГДР, разработанным по плану унификациистандартов двух стран.
В основу стандарта положены методы оценкипределов выносливости и других характеристик сопротивления усталости деталей,вошедшие в стандарты ГДР [1,5-7]и в справочные руководства СССР [2-4].
Излагаются методы оценки медианныхзначений пределов выносливости деталей 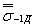 и их коэффициентоввариации
и их коэффициентоввариации 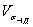 , что позволяет определять значения пределов выносливости (σ-1д)р, соответствующие заданной вероятности Р %.
, что позволяет определять значения пределов выносливости (σ-1д)р, соответствующие заданной вероятности Р %.
Наиболее точным методом определениякоэффициентов К, отражающихсуммарное влияние всех факторов на пределы выносливости, являетсяэкспериментальный метод (п.1.2.1).
Для расчетного определения эффективныхкоэффициентов концентрации Кσ, Кτиотношений Kσ/Kdσ., Kτ/Kdt предлагаются три метода, изложенные в порядкепредпочтительного использования, зависящего от имеющейся исходной информации.
Первый метод, изложенный в п.1.2.3.1, формулы (11),(12),основан на статистической теории подобия усталостного разрушения [4].Эта теория получила апробирование во многих лабораториях СССР в течениепоследних 20 лет и успешно используется в ряде отраслей машиностроения. Вслучае экспериментального определения коэффициентов vσ и vτ путем испытаний на усталость образцов и моделей встатистическом аспекте ошибка в оценке отношений Kσ/Kdσ не превышает 4 % с вероятностью 95 %. При испытанияхпо стандартной методике ограниченного числа образцов каждого типоразмера дляопределения v ошибка непревышает 8 % с вероятностью 95 %.
При затруднениях с определением параметраL, а, следовательно, и критерия подобия Θ, входящего в формулы (11), (12),рекомендуется использовать приближенный метод Зибеля и Штилера, представленныйформулами (13), (14), рекомендуемыйстандартом ГДР TGL 19340. Для этой же цели допускается применение формул(18), (19), основанных наиспользовании коэффициентов чувствительности металла к концентрации напряжений q, рекомендуемых в американской справочной литературе/8/, а также в ряде руководств в СССР. Следует иметь в виду, что формулы (13)-(19) приводят кпогрешностям существенно большим (до 20 %), чем формулы (11), (12).Формулы (29), (30) для коэффициентоввлияния качества обработки поверхности KFσ , KFτ формула (20) для коэффициентавлияния абсолютных размеров и формула (15) получены разработчиками стандарта ГДР Б. Хенелем, Г.Виртгеном и К. Шустером (Институт легких конструкций г. Дрезден) путемаппроксимации эмпирических графиков, приведенных в TGL 19340.
В разд. 3 стандарта изложен метод оценкикоэффициентов вариации пределов выносливости 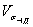 , вытекающий из теории подобия усталостного разрушения [4].В связи с оценкой коэффициентов
, вытекающий из теории подобия усталостного разрушения [4].В связи с оценкой коэффициентов 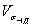 вводят два медианных значения пределавыносливости гладких лабораторных образцов диаметром d0 = 7,5 мм при изгибе с вращением σ-1 ,
вводят два медианных значения пределавыносливости гладких лабораторных образцов диаметром d0 = 7,5 мм при изгибе с вращением σ-1 , 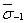 , определенное на образцах металла одной плавки, и
, определенное на образцах металла одной плавки, и 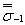 , определенное на множестве всех плавок металла данной марки.В связи с этим коэффициент вариации
, определенное на множестве всех плавок металла данной марки.В связи с этим коэффициент вариации 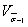 (формулы 35-37) учитывает межплавочный разброс величин
(формулы 35-37) учитывает межплавочный разброс величин 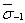 .
.
Известно, что с ростом размеров заготовкипри термообработке снижаются механические свойства металла (σв, σт, σ-1),определенные на лабораторных образцах малых размеров ([2],фиг. 41, стр. 129). В связи с этим вводят коэффициент К1 (формула (3)),равный отношению пределов выносливости 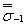 и
и 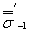 определенных налабораторных образцах диаметром d0 = 7,5мм, изготовленных из заготовок размером d (таким же, как размер натурной детали) и размером 10-20мм соответственно.
определенных налабораторных образцах диаметром d0 = 7,5мм, изготовленных из заготовок размером d (таким же, как размер натурной детали) и размером 10-20мм соответственно.
Теоретические коэффициенты концентрации ασ, ατ предлагаетсяопределять по номограммам и формулам Нейбера, по графикам, приведенным в работе[8],а также по приближенной формуле (25), заимствованной из TGL 19340.Последнюю формулу используют в случае необходимости вычислений ασ на ЭВМ.
Величины vσ, vτ, являющиесяпараметрами уравнения подобия усталостного разрушения [4],характеризуют чувствительность металла к концентрации напряжений и влиянию абсолютныхразмеров поперечного сечения. С ростом vσ чувствительностьк концентрации напряжений уменьшается, а влияние абсолютных размеров навеличины пределов выносливости усиливается.
Значения vσ, vτ находят экспериментально по методике, выбирают 4-5 илиболее типоразмеров образцов с различными значениями критерия подобияусталостного разрушения Θ (так,чтобы диапазон изменения Θ былпо возможности наибольшим). Находят пределы выносливости этих образцов, причемпредпочтительно методом «лестницы» или «пробит» - методом. По найденнымзначениям строят зависимость 1g (ξ - 1) от 1g Θ,соответствующую уравнению подобия [4].
1g (ξ - 1) =- vσ ∙ 1gΘ, (1)
где
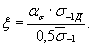
Значение 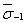 находят путемпредварительного построения зависимости σтах = ασ∙ σ-1д от 1g Θи ее осреднения. По зависимости (1), найденной методом наименьших квадратов, определяютзначение vσ.
находят путемпредварительного построения зависимости σтах = ασ∙ σ-1д от 1g Θи ее осреднения. По зависимости (1), найденной методом наименьших квадратов, определяютзначение vσ.
В случае невозможности проведенияэкспериментов значения vσ и vτ определяют по корреляционным зависимостям (27) и (28).
Расчетные характеристики для оценкидолговечности при малоцикловом нагружении определяют применительно к широкоиспользуемому подходу, основывающемуся на учете местных циклических деформацийв конструкциях. Расчет выполняют с привлечением деформационно-кинетическихкритериев малоцикловой прочности, трактующих достижение предельного состояния ввиде критических величин квазистатических и усталостных повреждений и их сумм влинейной форме. Расчет ведут в деформациях (циклических упругопластических иодносторонне накопленных).
Учитывают кинетику односторонне накопленныхи циклических деформаций в процессе нагружения в максимально напряженных зонахконструкции, а также деформационную способность материала при статическом(квазистатическом) и малоцикловом нагружениях. Первая характеризуетсярасполагаемой пластичностью, вторая - кривой малоцикловой усталостиконструкционного материала.
Изменяющиеся от цикла к циклу диаграммыдеформирования используют в форме обобщенной диаграммы, отражающей процессыциклического упрочнения, разупрочнения и стабилизации. Указанная обобщеннаядиаграмма вошла в практику расчетов при малоцикловом нагружении.
Задачу о напряженно-деформированномсостоянии элементов конструкций решают расчетным и экспериментальными методамив циклической упругопластической постановке.
Названные подходы систематически изложеныв ряде изданий [3, 9-11].
| [1] | DDR-Standard TGL 19340, Blatt I bis 4 (2 Entwurf, Juli 1974) Maschinenbauteile, Dauerschwingfestigkeit |
| [2] | Серенсен С.В., Когаев В.П., Шнейдерович P.M. Несущая способность и расчеты на прочность деталей машин. М., Машгиз, 1963, с. 451 |
| [3] | Серенсен С.В., Когаев В.П., Шнейдерович P.M. Несущая способность и расчеты на прочность деталей машин. М., «Машиностроение», 1975, с. 488 |
| [4] | Когаев В.П. Расчеты на прочность при напряжениях переменных во времени. М., «Машиностроение»,1977 |
| [5] | Hanel В., Wirthgen G. Neufassung des DDR - Standards TGL 19330 «Schwingfestigkeit, Begriffe und Zeichen». IfL-Mitt, Dresden, 18 (1979) 5, s. 178-191 |
| [6] | C. Schuster und C. Wirthgen. Aufbau und Anwendung der DDR-Standards TGL 19340 (Neufassung) «Maschinenbauteile, Dauerschwingfestig-keit», IfL-Mitt., Dresden, 14 (1975) Heft 1/2, s. 3-29 |
| [7] | B/Hanel und G. Wirthgen. Zum DDR-Standards TGL 36766 «Schwigfestigkeit, Ermudungspriifung von Werkstoffproben», IfL-Mitt., Dresden, 1979, 5, s. 211-215 |
| [8] | Петерсон Р.Е. Концентрация напряжений. М., «Мир», 1977, с. 302 |
| [9] | Москвитин В.В. Пластичность при переменных нагружениях. Изд. Моск. университета, 1965, с. 263 |
| [10] | Гусенков А.П. Прочность при изотермическом и неизотермическом малоцикловом нагружении. М.,«Наука», 1979, с. 295 |
| [11] | Махутов НА. Деформационные критерии разрушения и расчет элементов конструкций на прочность. М., «Машиностроение», 1981, с. 272 |
1. РАЗРАБОТАН Академиейнаук СССР, Государственным комитетом СССР по стандартам, Министерством высшегои среднего специального образования СССР, Министерством тракторного и сельскохозяйственногомашиностроения
2. УТВЕРЖДЕН И ВВЕДЕН ВДЕЙСТВИЕ ПОСТАНОВЛЕНИЕМ Государственного комитета СССР по стандартам от18.05.82 № 1972
3. Стандарт унифицирован состандартами ГДР TGL 19340/03 и TGL 19340/04
4. ВВЕДЕН ВПЕРВЫЕ
5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕДОКУМЕНТЫ
6. Ограничение срокадействия снято по протоколу № 3-93 Межгосударственного совета постандартизации, метрологии и сертификации (ИУС 5-6-93)
7. ИЗДАНИЕ с Изменением №1, утвержденным в декабре 1988г. (ИУС 4-89)
Новости
Библиотека
Soft по ОТ и ПБ
Консультации
Агрегатор
Услуги
Форум
Золотой фонд
ССОТ
CHAT-OT


.webp)


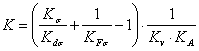
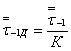
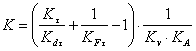
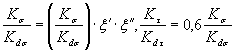

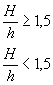
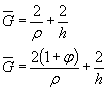
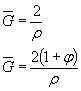

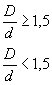
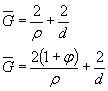
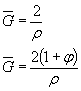
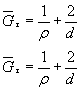

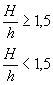
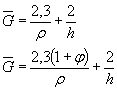

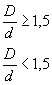
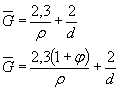
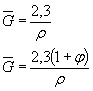
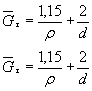
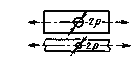
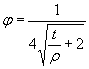






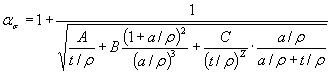
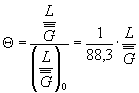
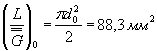
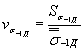
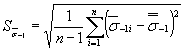
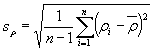
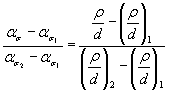

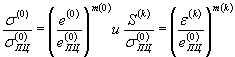
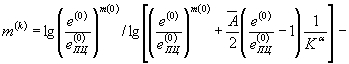
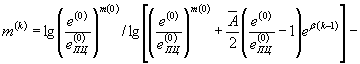
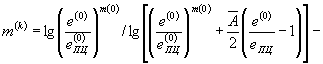
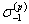
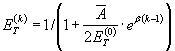
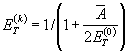








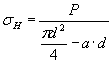













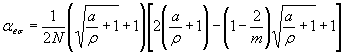



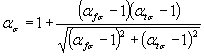
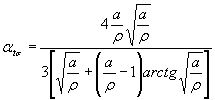





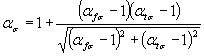
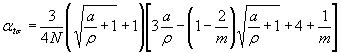
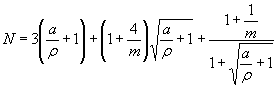



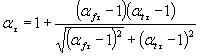
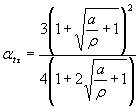 .
.